Cho hàm số y = f(x) = ( a,b,c,d , 0) đồ thị hàm số y= f’(x) như hình vẽ.
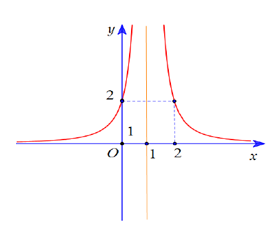
Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y =
B. y =
C. y =
D. y =
 Giải bởi Vietjack
Giải bởi Vietjack
+ Ta có = . Từ đồ thị hàm số y= f’(x) ta thấy:
Đồ thị hàm số y= f’(x) có tiệm cận đứng x=1 nên –d/c= 1 hay c= -d
Đồ thị hàm số y= f’(x ) đi qua điểm (2;2)
Đồ thị hàm số y= f’(x) đi qua điểm (0;2)
Đồ thị hàm số y=f(x) đi qua điểm (0;3) nên b/d= 3 hay b= 3d
Giải hệ gồm 4 pt này ta được a=c= -d và b= 3d .
Ta chọn a=c= 1 ; b= -3 ; d= -1
Chọn D.
Cho hàm số y = . Với tham số m bằng bao nhiêu thì thỏa mãn trên đoạn [1; 2].
Cho hàm số f(x) = với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 1] bằng – 2.
Cho hàm số y= f(x) xác định trên R và có đồ thị như hình bên. Hỏi phương trình f(|x-2|) = -1/2 có bao nhiêu nghiệm?
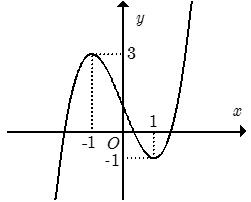
Cho hàm số f(x) = x3 - 3x2 + 2 có đồ thị là đường cong trong hình bên. Tìm tất cả các giá trị thực của tham số m đề phương trình có nhiều nghiệm thực nhất
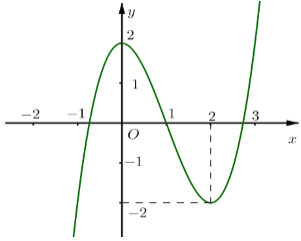
Cho hàm số y= f(x )= ax3+ bx2+ cx+ d có bảng biến thiên như sau:
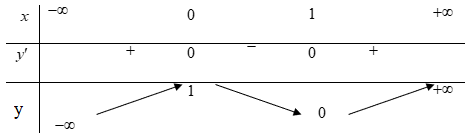
Khi đó |f(x)| = m có 4 nghiệm phân biệt khi và chỉ khi
Cho hàm số y= f(x) xác định trên R và có đồ thị như hình bên. Hỏi với những giá trị nào của tham số thực m thì phương trình có đúng hai nghiệm phân biệt.
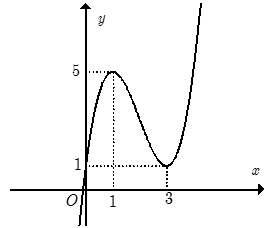
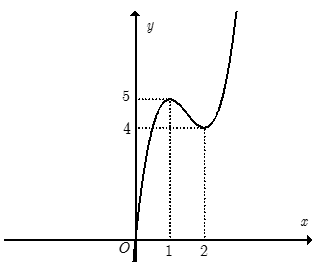
Hàm số y= 2x3-9x2+ 12x có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của tham số m để phương trình có sáu nghiệm phân biệt.
Tìm tất cả các giá trị thực của tham số m để hàm số y = liên tục và đạt cực tiểu trên [0;2] tại một điểm 0 < x0 < 2.
Tìm tổng tất cả các giá trị của tham số m sao cho giá trị lớn nhất của hàm số y = trên đoạn [-1; 2] bằng 5.
Cho hàm số y= f(x) xác định trên R và có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham số m để phương trình
2 - m = 0 có đúng bốn nghiệm phân biệt.
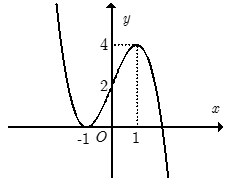
Hình vẽ bên là đồ thị của hàm số y= x3-3x-1. Tất cả các giá trị thực của m để phương trình có 3 nghiệm đôi một khác nhau là
Cho hàm số f(x) = với m là tham số thực. Tìm tất cả các giá trị của m > 1 để hàm số có giá trị lớn nhất trên đoạn [ 0; 4] nhỏ hơn 3.
Tìm tất cả các giá trị thực k đề phương trình = có đúng 4 nghiệm phân biệt.
Muốn làm một bồn chứa 1000 lít hình trụ có nắp đậy. Hỏi chiều cao h (dm) của bồn gần với giá trị nào nhất để ít tốn vật liệu nhất?