Trong không gian Oxyz, cho hình bình hành ABCD với A(0;1;-2), B(3;-2;1), D(1;4;2). Tọa độ của điểm C là:
A. (4;1;5)
B. (4;3;1)
C. (4;2;3)
D. (4;1;1)
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
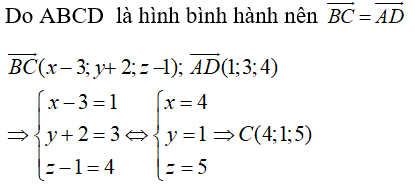
Vị trí tương đối của hai mặt cầu: + 2x - 2y - 2z - 7 = 0 và + 2x + 2y + 4z + 5 = 0 là:
Cho mặt cầu (S) có phương trình: - 2x + 4y - 6z - 2 = 0 . Điểm M(m; -2; 3) nằm trong mặt cầu khi và chỉ khi:
Trong không gian Oxyz, cho A(1;0;-3), B(-3;-2;-5). Biết rằng tập hợp các điểm M trong không gian thỏa mãn đẳng thức = 30 là một mặt cầu (S). Tìm tọa độ tâm I và bán kính R của (S).
Trong không gian Oxyz, ba điểm nào dưới đây lập thành ba đỉnh của một tam giác?
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
+ 6x - 8y + 15z - 3 = 0
Tìm tọa độ tâm I và bán kính R của mặt cầu (S).
Trong không gian cho hai điểm A(x; y; z), B(m, n, p) thay đổi nhưng luôn thỏa mãn các điều kiện = 4, = 9. Vectơ có độ dài nhỏ nhất là:
Trong không gian Oxyz, cho điểm G(1;2;3) là trọng tâm của tam giác ABC trong đó A thuộc trục Ox, B thuộc trục Oy, C thuộc trục Oz. Tọa độ các điểm A, B, C là:
Cho mặt cầu (S) có tâm I(1;2;3), bán kính R = 4. Khẳng định nào sau đây là đúng?
Cho (S) là mặt cầu có tâm I(1;2;4) và đi qua điểm M(-1;4;3). Khẳng định nào dưới đây sai?
Trong không gian Oxyz, cho vectơ = (1; -2; 3). Tìm tọa độ của vectơ biết rằng vectơ ngược hướng với vectơ
và || = 2||
Trong không gian Oxyz, cho vectơ = (m; m + 3; 3 - 2m). Với giá trị nào của m thì vectơ có độ dài nhỏ nhất
Trong không gian Oxyz, cho mặt cầu (S) đi qua bốn điểm O, A(-4;0;0), B(0;2;0), C(0;0;4). Phương trình của mặt cầu (S) là:
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là: = 4
Cho ba điểm A, M, B nằm trên mặt cầu (S) thỏa mãn điều kiện góc AMB = 90o. Diện tích tam giác AMB có giá trị lớn nhất là:
Cho mặt cầu (S) có tâm I(1;2;-1) và bán kính R=3. Phương trình mặt cầu (S’) đối xứng với mặt cầu (S) qua gốc tọa độ là: