30 câu hỏi trắc nghiệm thuộc 60 câu trắc nghiệm: Hệ tọa độ trong không gian có đáp án (P2)

Câu 1:

Trong không gian Oxyz, cho hai vectơ $\vec{a}$ = (1; -2; 2), $\vec{b}$ = (-2; m - 3; m). Với những giá trị nào của m thì hai vectơ $\vec{a}$ và $\vec{b}$ có độ dài bằng nhau?

A. m = 1 hoặc m = 2

B. m = 1

C. m = 2

D. Không có m

Xem đáp án

Đáp án A

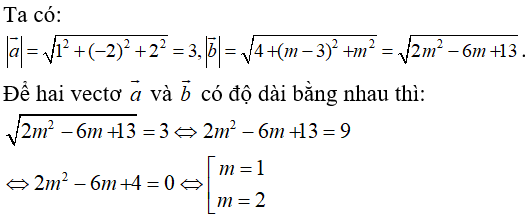
Câu 2:

Trong không gian Oxyz, cho điểm G(1;2;3) là trọng tâm của tam giác ABC trong đó A thuộc trục Ox, B thuộc trục Oy, C thuộc trục Oz. Tọa độ các điểm A, B, C là:

A. A(1; 0; 0), B(0; 2; 0), C(0; 0; 3)

B. A(3; 0; 0), B(0; 6; 0), C(0; 0; 9)

C. A(-3; 0; 0), B(0; -6; 0), C(0; 0; -9)

D. A(6; 0; 0), B(0; 3; 0), C(0; 0; 9)

Xem đáp án

Đáp án B

Do A thuộc trục Ox, B thuộc trục Oy, C thuộc trục Oz nên A(a; 0; 0); B(0; b; 0) và C(0; 0; c).

Mà điểm G(1;2;3) là trọng tâm của tam giác ABC nên:

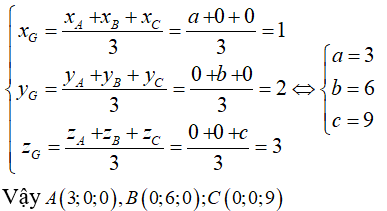
Câu 3:

Trong không gian Oxyz, ba điểm nào dưới đây lập thành ba đỉnh của một tam giác?

A. A(1; 2; 3), B(5; -4; -1), C(3; -1; 1)

B. A(1; 2; 3), B(5; -4; -1), C(6; -2; 2)

C. A(1; 2; 3), B(5; -4; -1), C(9; -10; -5)

D. A(1; 2; 3), B(5; -4; -1), C(-3; 8; 7)

Xem đáp án

Đáp án B

Để ba điểm A, B,C lập thành ba đỉnh của 1 tam giác khi và chỉ khi ba điểm A, B,C không thẳng hàng hay hai vecto $\vec{AB}$ ; $\vec{AC}$ không cùng phương

Xét phương án B ta có:

$\vec{AB}$ = (4; -6; -4); $\vec{AC}$ = (5; -4; -1)

Suy ra hai vecto này không cùng phương hay 3 điểm A, B, C không thằng hàng.

Câu 4:

Cho hai vectơ $\vec{a}, \vec{b}$ thay đổi nhưng luôn thỏa mãn

Giá trị lớn nhất của

A. 11

B. -1

C. 1

D. $\sqrt{61}$

Xem đáp án

Đáp án A

Sử dụng bất đẳng thức vectơ:

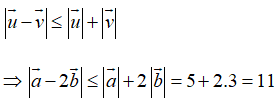
Dấu bằng xảy ra khi và chỉ khi hai vectơ này ngược hướng. Suy ra đáp án A.

Hai đáp án B và C xuất phát từ sai lầm

Câu 5:

Trong không gian cho hai điểm A(x; y; z), B(m, n, p) thay đổi nhưng luôn thỏa mãn các điều kiện $x^{2} + y^{2} + z^{2}$ = 4, $m^{2} + n^{2} + p^{2}$ = 9. Vectơ $\vec{AB}$ có độ dài nhỏ nhất là:

A. 5

B. 1

C. 13

D. Không tồn tại

Xem đáp án

Đáp án B

Từ giả thiết suy ra

Do đó AB ≥ |OA - OB| = 1. Dấu bằng xảy ra khi O nằm ngoài đoạn AB. Suy ra đáp án đúng là B.

Hai đáp án A, D sai do nhầm OA = $x^{2} + y^{2} + z^{2}$ = 4; OB = $m^{2} + n^{2} + p^{2}$ = 9

Đáp án C sai do nhầm với câu hỏi vectơ $\vec{A B}$ có độ dài lớn nhất

Câu 6:

Trong không gian Oxyz, cho hình bình hành ABCD với A(0;1;-2), B(3;-2;1), D(1;4;2). Tọa độ của điểm C là:

A. (4;1;5)

B. (4;3;1)

C. (4;2;3)

D. (4;1;1)

Xem đáp án

Đáp án A

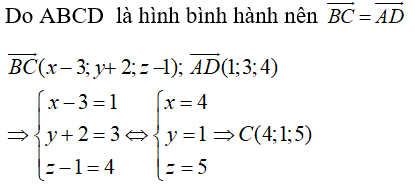
Câu 7:

Trong không gian Oxyz, cho hình hộp ABCD.A'B'C'D' có A(0;0;0), B(1;2;0), D(2;-1;0), A’(5;2;3). Tọa độ của điểm C’ là:

A. (3;1;0)

B. (8;3;3)

C. (-8;-3;-3)

D. (-2;-1;-3)

Xem đáp án

Đáp án B

Câu 8:

Trong không gian Oxyz, cho vectơ $\vec{a}$ = (1; -2; 3). Tìm tọa độ của vectơ $\vec{b}$ biết rằng vectơ $\vec{b}$ ngược hướng với vectơ $\vec{a}$

và | $\vec{b}$ | = 2| $\vec{a}$ |

A. $\vec{b} = (2; - 4; 6)$

B. $\vec{b} = (2; - 2; 3)$

C. $\vec{b} = (- 2; 4; - 6)$

D. $\vec{b} = (- 2; - 2; 3)$

Xem đáp án

Đáp án C

Vì vectơ $\vec{b}$ ngược hướng với vectơ $\vec{a}$ và | $\vec{b}$ | = 2| $\vec{a}$ | nên:

$\vec{b}$ = -2 $\vec{a}$ = (-2; 4; -6)

Câu 9:

Trong không gian Oxyz, cho vectơ $\vec{a}$ = (-1; -2; 3). Tìm tọa độ của vectơ $\vec{b}$ = (2; y; z) biết rằng vectơ $\vec{b}$ cùng phương với vectơ $\vec{a}$

A. $\vec{b} = (2; - 2; 3)$

B. $\vec{b} = (2; 4; 6)$

C. $\vec{b} = (2; - 4; 6)$

D. $\vec{b} = (2; 4; - 6)$

Xem đáp án

Đáp án D

Vectơ $\vec{b}$ cùng phương với vectơ $\vec{a}$ khi và chỉ khi tồn tại một số thực k thỏa mãn:

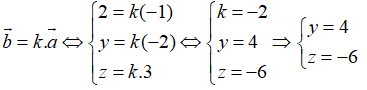
Câu 10:

Trong không gian Oxyz, cho vectơ $\vec{a}$ = (m; m + 3; 3 - 2m). Với giá trị nào của m thì vectơ $\vec{a}$ có độ dài nhỏ nhất

A. m = 1/2

B. m = 0

C. m = 1

D. m = -3

Xem đáp án

Đáp án A

Câu 11:

Trong không gian Oxyz, cho hai vectơ $\vec{u}$ = (3; 4; 0), $\vec{v}$ = (2; -1; 2) . Tích vô hướng của hai vectơ $\vec{u}$ và $\vec{v}$ là:

A. 15

B. 2

C. 3

D. 0

Xem đáp án

Đáp án B

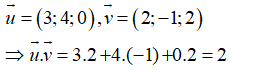
Câu 12:

Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:

${(x - 1)}^{2} + {(y + 2)}^{2} + {(z + 3)}^{2}$ = 25

Tìm tọa độ tâm I và bán kính R của mặt cầu (S)

A. I(1; -2; -3); R = 25

B. I(-1; 2; 3); R = 5

C. I(-1; 2; 3); R = 25

D. I(1; -2; -3); R = 5

Xem đáp án

Đáp án D

Câu 13:

Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:

$x^{2} + y^{2} + z^{2}$ - 2x + 4y + 4z + 5 = 0

Tìm tọa độ tâm I và bán kính R của mặt cầu (S)

A. I(1; -2; -2); R = 2

B. I(1; -2; -2); R = 4

C. I(-1; 2; 2); R = 2

D. I(-2; 4; 4); R = 4

Xem đáp án

Đáp án A

Câu 14:

Phương trình nào dưới đây là phương trình của một mặt cầu?

A. $x^{2} + y^{2} + z^{2}$ - 2x + 4y - 8z + 25 = 0

B. $x^{2} + y^{2} + z^{2}$ - 2x - 4y - 6z + 15 = 0

C. 3 $x^{2} + 3 y^{2} + 3 z^{2}$ - 6x - 7y - 8z + 1 = 0

D. ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z + 3)}^{2}$ + 10 = 0

Xem đáp án

Đáp án C

Sử dụng phương trình $x^{2} + y^{2} + z^{2}$ - 2ax - 2by - 2cz + d = 0 là phương trình của một mặt cầu khi và chỉ khi $a^{2} + b^{2} + c^{2}$ - d > 0

+ Phương án A và B không thỏa mãn điều kiện $a^{2} + b^{2} + c^{2}$ - d > 0

+ Phương án C: 3 $x^{2} + 3 y^{2} + 3 z^{2}$ - 6x - 7y - 8z + 1 = 0

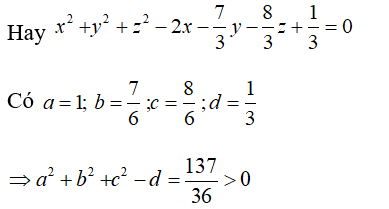
Nên đây có là phương trình mặt cầu.

+ Phương án D: ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2}$ + 10 = 0

⇔ ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2}$ = -10 nên không là phương trình mặt cầu.

Câu 15:

Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:

$3 x^{2} + 3 y^{2} + 3 z^{2}$ + 6x - 8y + 15z - 3 = 0

Tìm tọa độ tâm I và bán kính R của mặt cầu (S).

A. $I (- 1; \frac{4}{3}; - \frac{5}{2}), R = \frac{361}{36}$

B. $I (- 1; \frac{4}{3}; - \frac{5}{2}), R = \frac{19}{6}$

C. $I (- 3; 4; - \frac{15}{2}), R = \frac{19}{6}$

D. $I (3; - 4; \frac{15}{2}), R = \frac{361}{36}$

Xem đáp án

Đáp án B

Câu 16:

Trong không gian Oxyz, cho mặt cầu (S) có đường kính AB với A(-2;-4;3), B(4;2;0). Tìm tọa độ tâm I và bán kính R của mặt cầu (S).

A. $I (1; - 1; \frac{3}{2}), R = 9$

B. $I (2; - 2; 3), R = \frac{9}{2}$

C. $I (1; - 1; \frac{3}{2}), R = \frac{9}{2}$

D. $I (2; - 2; 3), R = 9$

Xem đáp án

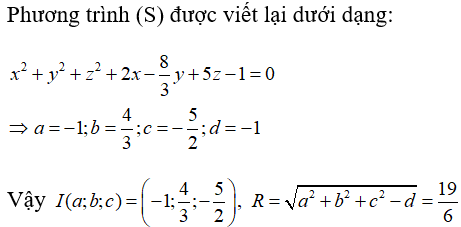
Câu 17:

Trong không gian Oxyz, cho mặt cầu (S) có tâm I(1;-2;-3) và đi qua điểm M(-1;0;-2). Phương trình của mặt cầu (S) là:

A. ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z + 3)}^{2}$ = 3

B. ${(x + 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2}$ = 9

C. ${(x + 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2}$ = 3

D. ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z + 3)}^{2}$ = 9

Xem đáp án

Đáp án D

Câu 18:

Cho (S) là mặt cầu có tâm I(1;2;4) và đi qua điểm M(-1;4;3). Khẳng định nào dưới đây sai?

A. Bán kính của mặt cầu (S) là R = IM = 3

B. Phương trình chính tắc của mặt cầu (S) là: ${(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 4)}^{2}$ = 9

C. Mặt cầu (S) đi qua gốc tọa độ

D. Phương trình tổng quát của mặt cầu (S) là: $x^{2} + y^{2} + z^{2}$ - 2x - 4y - 8z + 12 = 0

Xem đáp án

Đáp án C

Ta có: .

Suy ra:

* Bán kính của mặt cầu (S) là R = IM = 3

* Phương trình chính tắc của mặt cầu (S) là:

(x - 1)² + (y - 2)² + (z - 4)² = 9

* Phương trình tổng quát của mặt cầu (S) là:

$x^{2} + y^{2} + z^{2}$ - 2x - 4y - 8z + 12 = 0

* Thay tọa độ điểm O vào phương trình mặt cầu ta thấy không thỏa mãn nên mặt cầu không đi qua gốc tọa độ O.

Câu 19:

Cho mặt cầu (S) có tâm I(1;2;3), bán kính R = 4. Khẳng định nào sau đây là đúng?

A. Diện tích của mặt cầu (S) bằng 16π

B. Thể tích của khối cầu (S) bằng 64π/3

C. Phương trình chính tắc của (S) là: ${(x + 1)}^{2} + (y + 2)^{2} + {(z + 3)}^{2}$ = 16

D. Phương trình tổng quát của mặt cầu (S) là: $x^{2} + y^{2} + z^{2}$ - 2x - 4y - 6z - 2 = 0

Xem đáp án

Đáp án D

Mặt cầu (S) có tâm I(1; 2; 3), bán kính R = 4.

+) Diện tích của mặt cầu (S) là:

S = $4 π R^{2} = 4 π . 4^{2} = 64 π$

+) Thể tích của khối cầu (S) là:

V = $\frac{4}{3} π R^{3} = \frac{4}{3} . π . 4^{3} = \frac{256}{3} π$

+) Phương trình chính tắc của (S) là:

${(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 16$

+) Phương trình tổng quát của (S) là:

$x^{2} + y^{2} + z^{2} - 2 x - 4 y - 6 z - 2 = 0$

Câu 20:

Cho mặt cầu (S) có tâm I(1;2;-1) và bán kính R=3. Phương trình mặt cầu (S’) đối xứng với mặt cầu (S) qua gốc tọa độ là:

A. ${(x - 1)}^{2} + {(y - 2)}^{2} + (z + 1)^{2}$ = 9

B. ${(x + 1)}^{2} + {(y + 2)}^{2} + {(z - 1)}^{2}$ = 9

C. $x^{2} + y^{2} + z^{2}$ - 2x - 4y + 2z - 3 = 0

D. $x^{2} + y^{2} + z^{2}$ = 9

Xem đáp án

Đáp án B

Mặt cầu (S’) đối xứng với mặt cầu (S) qua gốc tọa độ nên mặt cầu (S’) có tâm I’(-1;-2; 1) đối xứng với I qua gốc O và có bán kính R’ = R = 3.

Phương trình mặt cầu (S’) là: ${(x + 1)}^{2} + {(y + 2)}^{2} + {(z - 1)}^{2}$ = 9

Câu 21:

Cho mặt cầu (S) có phương trình: $x^{2} + y^{2} + z^{2}$ - 2x + 4y - 6z - 2 = 0 . Điểm M(m; -2; 3) nằm trong mặt cầu khi và chỉ khi:

A. m=6

B. m > -3

C. -3 < m < 5

D. m < 5

Xem đáp án

Đáp án C

Câu 22:

Trong không gian Oxyz, cho mặt cầu (S) có tâm I(0;0;1), bán kính R=5. Mặt phẳng (P): 4x - 4y + z + m = 0 cắt mặt cầu (S) theo một đường tròn có bán kính bằng 5. Khi đó m bằng:

A. m=-1

B. m=-4

C. m=3

D. Đáp số khác

Xem đáp án

Đáp án A

Do mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn có bán kính bằng 5 bằng bán kính mặt cầu nên tâm I thuộc mặt phẳng (P).

Thay tọa độ tâm I vào phương trình mặt phẳng (P) ta được:

4.0 - 4.0 + 1+ m= 0 nên m = -1.

Câu 23:

Trong không gian Oxyz, cho mặt cầu (S) đi qua bốn điểm O, A(4;0;0), B(0;-2;0), C(0;0;2). Phương trình của mặt cầu (S) là:

A. ${(x - 1)}^{2} + {(y + 1)}^{2} + {(z - 1)}^{2}$ = 6

B. ${(x - 2)}^{2} + {(y + 1)}^{2} + {(z - 1)}^{2}$ = 24

C. ${(x - 4)}^{2} + {(y + 2)}^{2} + {(z + 2)}^{2}$ = 24

D. ${(x - 2)}^{2} + {(y + 1)}^{2} + {(z - 1)}^{2}$ = 6

Xem đáp án

Đáp án D

Câu 24:

Trong không gian Oxyz, cho mặt cầu (S) đi qua bốn điểm O, A(-4;0;0), B(0;2;0), C(0;0;4). Phương trình của mặt cầu (S) là:

A. $x^{2} + y^{2} + z^{2}$ + 2x - y - 2z = 0

B. $x^{2} + y^{2} + z^{2}$ + 4x + 2y - 4z = 0

C. $x^{2} + y^{2} + z^{2}$ + 4x - 2y + 4z = 0

D. $x^{2} + y^{2} + z^{2}$ + 4x - 2y - 4z = 0

Xem đáp án

Đáp án D

Phương trình tổng quát của mặt cầu (S) có dạng $x^{2} + y^{2} + z^{2}$ - 2ax - 2by - 2cz + d = 0 với $a^{2} + b^{2} + c^{2}$ - d > 0

Ta có: O(0; 0; 0) ∈ (S) ⇔ d = 0

A(-4; 0; 0) ∈ (S) ⇔ $(- 4)^{2} + 0^{2} + 0^{2}$ - 2a.(-4) - 0 - 0 + 0 = 0 ⇔ a = -2

B(0; 2; 0) ∈ (S) ⇔ $0^{2} + 2^{2} + 0^{2}$ - 0 - 2b.2 - 0 + 0 = 0 ⇔ b = 1

C(0; 0; 4) ∈ (S) ⇔ $0^{2} + 0^{2} + 4^{2}$ - 0 - 0 - 2c.4 - 0 = 0 ⇔ c = 2

Vậy phương trình tổng quát của mặt cầu (S) là: $x^{2} + y^{2} + z^{2}$ + 4x -2y - 4z = 0

Câu 25:

Vị trí tương đối của hai mặt cầu (S) có tâm I(1;1;1), bán kính R = 1 và mặt cầu (S’) có tâm I'(3;3;3), bán kính R’=1 là:

A. ở ngoài nhau

B. tiếp xúc

C. cắt nhau

D. chứa nhau

Xem đáp án

Đáp án A

Do đó, hai mặt cầu đã cho ở ngoài nhau.

Câu 26:

Vị trí tương đối của hai mặt cầu: $x^{2} + y^{2} + z^{2}$ + 2x - 2y - 2z - 7 = 0 và $x^{2} + y^{2} + z^{2}$ + 2x + 2y + 4z + 5 = 0 là:

A. ở ngoài nhau

B. tiếp xúc

C. cắt nhau

D. chứa nhau

Xem đáp án

Đáp án C

Mặt cầu: $x^{2} + y^{2} + z^{2}$ + 2x - 2y – 2z – 7 = 0 có tâm I(-1; 1;1) và R = $\sqrt{10}$

Mặt cầu: $x^{2} + y^{2} + z^{2}$ + 2x + 2y + 4z + 5= 0 có tâm I’( -1; -1; -2) và R’ = 1

$I I' = \sqrt{{(- 1 - (- 1))}^{2} + {(- 1 - 1)}^{2} + {(- 2 - 1)}^{2}} = \sqrt{13} < \sqrt{10} + 1 = R + R'$

Do đó, hai mặt cầu này cắt nhau.

Câu 27:

Trong không gian Oxyz, cho A(1;0;-3), B(-3;-2;-5). Biết rằng tập hợp các điểm M trong không gian thỏa mãn đẳng thức ${AM}^{2} + {BM}^{2}$ = 30 là một mặt cầu (S). Tìm tọa độ tâm I và bán kính R của (S).

A. I(-1; -1; -4); R = $\sqrt{9}$

B. I(-2; -2; -8); R = 3

C. I(-1; -1; -4); R = $\sqrt{30}$ /2

D. I(-1; -1; -4); R = 3

Xem đáp án

Chọn D

Gọi tọa độ điểm M(x;y;z)

là phương trình của mặt cầu (S), có tâm I (-1;-1;-4) và bán kính R = 3

Câu 28:

Trong không gian Oxyz, cho hai điểm A(0;2;-4), B(-3;5;2). Tìm tọa độ điểm M sao cho biểu thức ${AM}^{2} + 2 {BM}^{2}$ đạt giá trị nhỏ nhất.

A. M(-3/2; 7/2; -1)

B. M(-1; 3; -2)

C. M(-2; 4; 0)

D. M(-3; 7; -2)

Xem đáp án

Đáp án C

Gọi M(x; y; z). Ta có:

${AM}^{2} + 2 {BM}^{2} = x^{2} + {(y - 2)}^{2} + {(z + 4)}^{2} + 2 [{(x + 3)}^{2} + {(y - 5)}^{2} + {(z - 2)}^{2}]$

= $x^{2} + y^{2}$ - 4y + 4+ $z^{2}$ +8z+ 16 + 2( $x^{2}$ + 6x + 9 + $y^{2}$ – 10y + 25 + $z^{2}$ – 4z + 4)

= 3(x² + y² + z² + 4x - 8y) + 96 = 3[(x + 2)² + (y - 4)² + z²] + 36 ≥ 36

Dấu bằng xảy ra khi và chỉ khi x = -2, y = 4, z = 0 → M(-2; 4; 0).

Vậy đáp án đúng là C

Câu 29:

Trong không gian Oxyz, cho mặt cầu (S) có phương trình là: ${(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 3)}^{2}$ = 4

Cho ba điểm A, M, B nằm trên mặt cầu (S) thỏa mãn điều kiện góc AMB = 90^o. Diện tích tam giác AMB có giá trị lớn nhất là:

A. 4

B. 2

C. 4π

D. Không tồn tại

Xem đáp án

Đáp án A

Ba điểm A, M, B nằm trên mặt cầu (S) thỏa mãn điều kiện $\hat{A M B}$ = 90°

Nên tam giác AMB vuông tại M.

Ta có: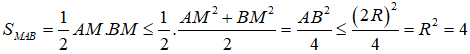

Dấu bằng xảy ra khi và chỉ khi tam giác MAB vuông cân tại M và AB là một đường kính của mặt cầu (S). Vậy đáp án đúng là A.

Câu 30:

Trong không gian Oxyz, cho hai mặt cầu (S) và (S’) có tâm lần lượt là I(-1;2;3), I’(3;-2;1) và có bán kính lần lượt là 4 và 2. Cho điểm M di động trên mặt cầu (S), N di động trên mặt cầu (S’). Khi đó giá trị lớn nhất của đoạn thẳng MN bằng:

A. 8

B. 2

C. 12

D. 6

Xem đáp án

Đáp án C

Ta có: II' = 6 = R + R'

Ta có: MN $\leq$ MI + II' + I'N = R + 6 + R' = 12

Dấu bằng xảy ra khi M, I, I', N theo thứ tự nằm trên một đường thẳng. Do đó M là giao điểm của tia đối của tia II' với mặt cầu (S), N là giao điểm của tia đối của tia I’I với mặt cầu (S’). Vậy đáp án đúng là C.