Hình nón tròn xoay ngoại tiếp tứ diện đều SABC cạnh a, có diện tích xung quanh là:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C
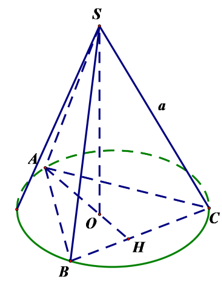
Gọi O là tâm của đường tròn đáy ⇒ SO ⊥ (ABC)
Ta có:
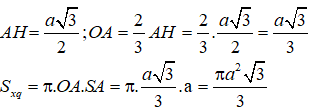
Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình nón. Diện tích xung quanh của hình nón đó là :
Cắt khối nón bởi một mặt phẳng qua trục tạo thành một tam giác ABC đều có cạnh bằng a, biết B, C thuộc đường tròn đáy. Thể tích của khối nón là:
Trong không gian, cho tam giác ABC cân tại A, Gọi H là trung điểm của BC. Tính thể tích V của hình nón nhận được khi quay tam giác ABC xung quanh trục AH.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy . Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là:
Một hình nón có đường cao h = 20cm, bán kính đáy r = 25cm. Tính diện tích xung quanh của hình nón đó:
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc . Thể tích của hình nón đỉnh S đáy là đường tròn ngoại tiếp ABCD là: