II. Tự luận ( 4 điểm)
Tính bán kính của mặt cầu ngoại tiếp hình chóp tam giác đều S.ABC, biết các cạnh đáy có độ dài bằng a, cạnh bên .
 Giải bởi Vietjack
Giải bởi Vietjack
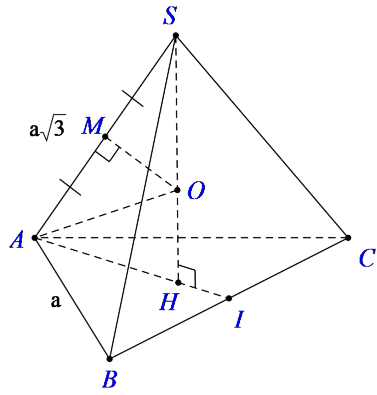
Gọi H là tâm của tam giác đều ABC.
Ta có SH ⊥ (ABC) nên SH là trục của tam giác ABC
Gọi M là trung điểm của SA, trong mp (SAH) kẻ trung trực của SA cắt SH tại O thì OS = OA (1)
Lại có, SH là trục của tam giác ABC và O ∈ SH nên: OA = OB = OC (2)
Từ (1) và (2) suy ra: OS = OA = OB = OC
Nên O chính là tâm mặt cầu ngoại tiếp hình chóp S.ABC.
Bán kính mặt cầu là R = SO.
Vì hai tam giác SMO và SHA đồng dạng nên ta có 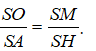
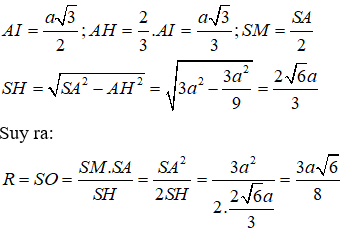
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc . Thể tích của hình nón đỉnh S đáy là đường tròn ngoại tiếp ABCD là:
Một hình nón có bán kính đáy bằng R, đường cao . Khi đó, góc ở đỉnh của hình nón là 2α. Khi đó khẳng định nào sau đây là khẳng định đúng ?
Một khối nón tròn xoay có độ dài đường sinh l = 13 cm và bán kính đáy r = 5cm. Khi đó thể tích khối nón là:
Một hình nón có đường kính đáy là , góc ở đỉnh là 120°. Tính thể tích của khối nón đó theo a
Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình nón. Diện tích xung quanh của hình nón đó là :
Cho hình nón đỉnh S, đường cao SO. Gọi A, B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng a và . Tính diện tích xung quanh hình nón.
Tính diện tích xung quanh của hình trụ có đường cao h = a và thể tích
I. Trắc nghiệm ( 6 điểm)
Một mặt cầu có đường kính 11m thì diện tích của mặt cầu là bao nhiêu? (lấy và làm tròn kết quả đến chữ số thập phân thứ hai).
Tính diện tích toàn phần của hình trụ có bán kính đáy a và đường cao .