Có bao nhiêu số phức z thỏa mãn và là số thuần ảo.
A. 2
B. 3
C. 4
D. 1
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C
Gọi z = x + yix, y ∈ R
![]()
![]()
z2 = (x2 - y2) + 2xyi là số thuần ảo khi và chỉ khi x2 - y2 = 0 (2)
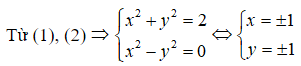
=> Có 4 số phức thỏa yêu cầu đề bài.
Cho số phức z có phần ảo gấp hai phần thực và . Khi đó mô đun của z là
Cho số phức , m nguyên dương. Có bao nhiêu giá trị m ∈ [1;50] để z là số thuần ảo?
Cho số phức Điểm biểu diễn số phức liên hợp của z trong mặt phẳng phức là:
Trong các số phức z thỏa mãn điều kiện . Số phức z có môđun nhỏ nhất là?
Tập hợp các điểm biểu diễn số phức là đường tròn . Tập hợp các điểm biểu diễn số phức z là đường tròn nào sau đây ?
Cho A, B, C là ba điểm trong mặt phẳng phức theo thứ tự biểu diễn các số:Tính
Trong mặt phẳng phức cho hai điểm Điểm C thỏa mãn: . Khi đó điểm C biểu diễn số phức: