Cho hàm số y = log2( 4x - 2x + m) có tập xác định D = R khi:
A.
B. m > 1/4
C. m < -1/4
D. m > 0
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn B.
Hàm số có tập xác định là D = R khi và chỉ khi 4x - 2x + m > 0 mọi x. (*)
Đặt t = 2x > 0 khi đó (*) trở thành : t2 – t + m > 0 mọi t > 0.
Hay m > t - t2 mọi t > 0
Ta có suy ra
Tìm tất cả các giá trị của tham số m sao cho hàm số đồng biến trên khoảng
Hỏi có bao nhiêu giá trị nguyên của m để phương trình 3x+m2=10m-9 có nghiệm thực?
Trong hình vẽ bên đồ thị (1) là của hàm số y = logax và đồ thị (2) là của hàm số y = logbx. Khẳng định nào sau đây là đúng.
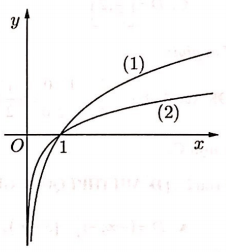
Cho hai số thực dương a ; b khác 1 Biết rằng bất kì đường thẳng nào song song với trục hoành mà cắt các đường y = ax; y =bx và trục tung lần lượt tại M ; N ; A thì AN = 3AM ( hình vẽ bên ).
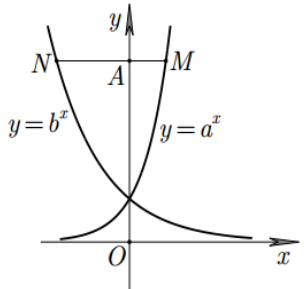
Hỏi khẳng định nào sau đây đúng ?
Cho hàm số có giá trị nhỏ nhất trên [1; e] bằng -3. Chọn khẳng định đúng về tham số m?
có tập xác định D = R khi đó có bao nhiêu giá trị nguyên dương của tham số m ?