Xét các số phức z thỏa mãn . Tìm số phức w có mô đun lớn nhất, biết rằng
A. w = 4 - 2i
B. w = -2 + 4i
C. w = 4 - 3i
D. w = 4 + 3i
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
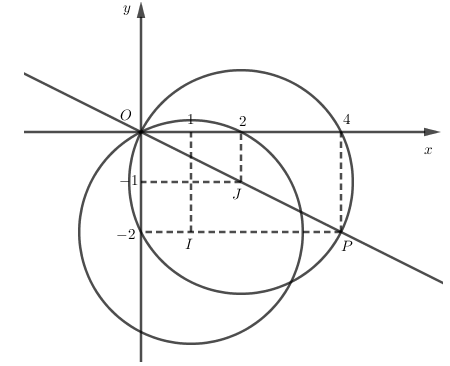
Các điểm M(x; y) biểu diễn z = x + yi có khoảng cách đến điểm I(1; - 2) biểu diễn 1 – 2i bằng nên thuộc đường tròn tâm I bán kính bằng
Từ đó các điểm biểu diễn w thay đổi trên đường tròn tâm J biểu diễn 1 – 2i + 1 + i = 2 - i, bán kính bằng .
Do nên đường tròn này đi qua gốc O
Điểm P biểu diễn w có mô đun lớn nhất khi P là điểm xuyên tâm đối của O trên đường tròn đó tức là w = 2(2 - i) = 4 – 2i
Xét số phức z thỏa mãn |z + 2 - i +|z - 4 - 7i| = . Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của |z - 1 + i|. Tính P = m + M
Cho các số phức thỏa mãn và . Gọi A, B lần lượt là điểm biểu diễn các số phức . Tính diện tích S của tam giác OAB với O là gốc tọa độ.
Gọi S là tổng phần thực và phần ảo của số phức , biết z thỏa mãn . Mệnh đề nào sau đây đúng?
Hỏi có bao nhiêu số phức thỏa mãn đồng thời các điều kiện và là số thuần ảo?
Tìm tập hợp các điểm trên mặt phẳng tọa độ biểu diễn các số phức z thỏa mãn điều kiện
Cho các số phức z thỏa mãn |z + 1 - i| = |z - 1 + 2i|. Tập hợp các điểm biểu diễn các số phức z trên mặt phẳng tọa độ là một đường thẳng. Viết phương trình đường thẳng đó