Cho số phức z thỏa mãn và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức là một trong bốn điểm M, N, P, Q. Khi đó điểm biểu diễn của số phức w là:
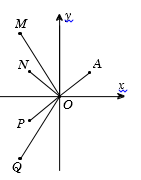
A. Điểm M.
B. Điểm N.
C. Điểm P.
D. Điểm Q.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án cần chọn là: C
Gọi . Từ giả thiết ta có
Ta có:
Vì x > 0, y > 0 nên điểm biểu diễn số phức w có tọa độ là (đều có hoành độ và tung độ âm).
Đồng thời
Suy ra, điểm biểu diễn của số phức w nằm trong góc phần tư thứ III và cách gốc tọa độ O một khoảng bằng OA.
Quan sát hình vẽ ta thấy có điểm P thỏa mãn.
Cho số phức z có tích phần thực và phần ảo bằng 625. Gọi a là phần thực của số phức . Giá trị nhỏ nhất của bằng.
Cho các số phức z thỏa mãn . Biết rằng tập hợp các điểm biểu diễn số phức là một đường tròn. Tính bán kính r của đường tròn đó.
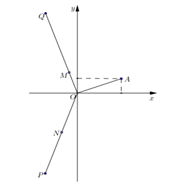
Cho số phức z thỏa mãn và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức là một trong bốn điểm M, N, P, Q. Khi đó điểm biểu diễn của số phức w là:
Cho hai số phức khác 0 thỏa mãn là số thuần ảo và . Giá trị lớn nhất của bằng:
Cho số phức z thay đổi, luôn có . Khi đó tập hợp điểm biểu diễn số phức là: