Trong không gian Oxyz, cho hai điểm A (1;0;0), B (0;0;2) và mặt cầu (S): x²+y²+z²-2x-2y+1=0. Hỏi có tất cả bao nhiêu mặt phẳng chứa hai điểm A, B và tiếp xúc với (S).
A.3.
B. 0
C. 1
D. 2
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C
Gọi (P) là mặt phẳng thỏa mãn bài toán.
Ta có A (1; 0; 0) ∈ (S) => nếu tồn tại (P) thì (P) tiếp xúc với (S) tại A.
Ta thấy B (0; 0 ; 2) ∈ (P)
Nên có duy nhất một mặt phẳng (P) thỏa mãn bài toán.
Ghi chú: Bài toán dạng này thường thì sẽ có hai mặt phẳng thỏa mãn, nhưng với số liệu của bài này thì chỉ có một mặt phẳng thỏa mãn bài toán.
Trong không gian Oxyz cho mặt cầu (S): (x - 1)² + (y - 2)² + (z - 3)² = 9 và mặt phẳng (P): 2x - 2y + z + 3 = 0. Gọi M (a; b; c) là điểm trên mặt cầu sao cho khoảng cách từ M đến (P) lớn nhất. Khi đó:
Trong không gian Oxyz, cho tam giác ABC với A (3;0;0), B (0;6;0), C (0;0;6). Phương trình nào dưới đây là phương trình đường thẳng đi qua trực tâm của tam giác ABC và vuông góc với mặt phẳng (ABC).
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng , mặt phẳng (α): x+y-z+3=0 và điểm A (1;2;-1). Viết phương trình đường thẳng Δ đi qua A cắt d và song song với mặt phẳng (α).
Trong không gian Oxyz, cho mặt cầu (S): (x -1)²+ (y + 2)² + (z - 3)² = 27. Gọi (α) là mặt phẳng đi qua hai điểm A (0; 0; -4), B (2; 0; 0) và cắt (S) theo giao tuyến là đường tròn (C) sao cho khối nón đỉnh là tâm của (S) và đáy là là đường tròn (C) có thể tích lớn nhất. Biết rằng (α): ax + by - z + c = 0, khi đó a - b + c bằng:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I (1;0;-1) và cắt mặt phẳng (P): 2x+y-2z-16=0 theo giao tuyến là một đường tròn có bán kính bằng 3. Phương trình của mặt cầu (S) là:
Trong không gian Oxyz cho điểm M (1;3;-2). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục x'Ox, y'Oy, z'Oz lần lượt tại ba điểm phân biệt A, B, C sao cho OA = OB = OC ≠ 0.
Trong không gian Oxyz, cho mặt phẳng (P):x+y+z-1=0 và hai điểm A (1;-3;0), B (5;-1;-2). Điểm M (a;b;c) nằm trên (P) và |MA – MB| lớn nhất. Giá trị abc bằng:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=9 và đường thẳng . Phương trình mặt phẳng (P) đi qua điểm M (4;3;4) song song với đường thẳng ∆ và tiếp xúc với mặt cầu (S) là:
Cho hình lập phương ABCD. A'B'C'D', gọi M và N lần lượt là tâm của các hình vuông ABCD và DCC'D'. Mặt phẳng (A'MN) chia khối lập phương trình hai phần có thể tích là V₁ và V₂ (V₁ < V₂). Tính tỷ số V₂/V₁
Trong không gian Oxyz cho mặt phẳng (P): 5x + my + 4z + n = 0 đi qua giao tuyến của hai mặt phẳng (α): 3x - 7y + z - 3 = 0 và (β): x - 9y - 2z + 5 = 0. Tính m + n.
Trong không gian Oxyz, cho đường thẳng và mặt phẳng (P):2x-3y+z-6=0. Phương trình nào dưới đây là phương trình của đường thẳng nằm trong mặt phẳng (P), cắt và vuông góc với (d)?
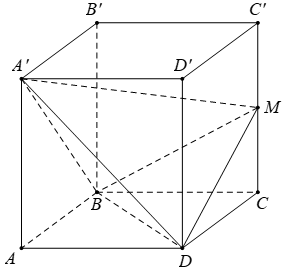
Cho hình hộp chữ nhật ABCD. A'B'C'D' có đáy ABCD là hình vuông cạnh a, AA'=b. Gọi M là trung điểm của cạnh CC'. Tính theo a và b thể tích V của khối tứ diện BDA'M
Trong không gian Oxyz, cho hai đường thẳng chéo nhau và . Phương trình nào dưới đây là phương trình đường thẳng vuông góc chung của d và d'?
Trong không gian tọa độ Oxyz cho A (1; 1; -1), B (2; 3; 1), C (5; 5; 1). Đường phân giác trong góc A của tam giác ABC cắt mặt phẳng (Oxy) tại M (a; b; 0). Tính 3b-a.
Trong không gian với hệ tọa độ Oxyz cho ba điểm A (3;-2;4), B (5; 3;-2), C (0;4;2), đường thẳng d cách đều ba điểm A, B, C có phương trình là: