Trong không gian Oxyz, cho bốn đường thẳng ;;; . Số đường thẳng trong không gian cắt cả bốn đường thẳng trên là:
A. 0.
B. 2.
C. Vô số.
D. 1.
Giải bởi Vietjack
Chọn D
Đường thẳng d₁ đi qua điểm M₁ = (3;-1;-1) và có một véctơ chỉ phương là 
Đường thẳng d₂ đi qua điểm M₂ = (0;0;1) và có một véctơ chỉ phương là 
Do 
và M₁ ∉ d₁ nên hai đường thẳng d₁ và d₂ song song với nhau.
Gọi (α) là mặt phẳng chứa d₁ và d₂ khi đó (α) có một véctơ pháp tuyến là 
. Phương trình mặt phẳng (α) là x+y+z-1=0.
Do 
không cùng phương với 
nên đường thẳng AB cắt hai đường thẳng d₁ và d₂.
Vậy có 1 đường thẳng cắt cả bốn đường thẳng trên
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;1;0) và đường thẳng .Phương trình tham số của đường thẳng d đi qua M, cắt và vuông góc với Δ là:
Trong không gian tọa độ Oxyz, cho tam giác ABC biết A (1;0;-1), B (2;3;-1), C (-2;1;1). Phương trình đường thẳng đi qua tâm đường tròn ngoại tiếp của tam giác ABC và vuông góc với mặt phẳng (ABC) là:
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;2;3) và mặt phẳng (P): 2x+y-4z+1=0, đường thẳng d đi qua điểm A, song song với mặt phẳng (P), đồng thời cắt trục Oz. Viết phương trình tham số của đường thẳng d.
Trong không gian Oxyz, cho điểm M (1;1;2). Mặt phẳng (P) qua M cắt các tia Ox, Oy, Oz lần lượt tại A, B, C sao cho thể tích tứ diện OABC nhỏ nhất. Gọi 
là một véc tơ pháp tuyến của (P). Tính S = a³ - 2b.
Trong không gian với hệ tọa độ Oxyz, cho (P): x - 2y + 2z - 5 = 0, A (-3;0;1), B (1;-1;3). Viết phương trình đường thẳng d đi qua A, song song với (P) sao cho khoảng cách từ B đến d là lớn nhất.
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+ (y+1)²+ (z-2)²= 16 và điểm A (1;2;3). Ba mặt phẳng thay đổi đi qua I là tâm của mặt cầu (S) và đôi một vuông góc với nhau, cắt mặt cầu theo ba đường tròn. Tính tổng diện tích của ba đường tròn tương ứng đó.
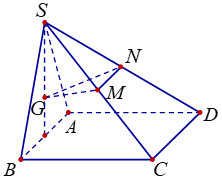
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Gọi G là trọng tâm của tam giác SAB và M, N lần lượt là trung điểm của SC, SD. Tính côsin của góc giữa hai mặt phẳng (GMN) và (ABCD).
Trong không gian Oxyz, mặt cầu (S) tâm I (2; 5; 3) cắt đường thẳng 
tại hai điểm phân biệt A, B với chu vi tam giác IAB bằng 10 + . Phương trình nào sau đây là phương trình của mặt cầu (S)?
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng và . Trên đường thẳng d₁ lấy hai điểm A, B thỏa mãn AB=3. Trên đường thẳng d₂ lấy hai điểm C, D thỏa mãn CD=4. Tính thể tích V của tứ diện ABCD.
Trong không gian tọa độ Oxyz, cho các điểm A (1;2;3), B (2;1;0), C (4;3;-2), D (3;4;1), E (1;1;-1). Hỏi có bao nhiêu mặt phẳng cách đều 5 điểm trên?
Trong không gian với hệ tọa độ Oyz cho điểm A (2;1;3) và mặt phẳng (P): x+my+ (2m+1)z-m-2=0, m là tham số. Gọi H (a;b;c) là hình chiếu vuông góc của điểm A trên (P). Tính a+b khi khoảng cách từ điểm A đến (P) lớn nhất?
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A (2;-3;2), B (3;5;4). Tìm toạ độ điểm M trên trục Oz so cho MA²+MB² đạt giá trị nhỏ nhất.
Trong không gian Oxyz, cho đường thẳng và mặt phẳng (α): x+y-z-2=0. Trong các đường thẳng sau, đường thẳng nào nằm trong mặt phẳng (α), đồng thời vuông góc và cắt đường thẳng d?
Trong không gian Oxyz, cho mặt phẳng (α): 2x+y-2z-2=0, đường thẳng và điểm . Gọi Δ là đường thẳng nằm trong mặt phẳng (α), song song với d đồng thời cách d một khoảng bằng 3. Đường thẳng ∆ cắt mặt phẳng (Oxy) tại điểm B. Độ dài đoạn thẳng AB bằng:
Trong không gian tọa độ Oxyz, cho điểm A (0;0;-2) và đường thẳng . Phương trình mặt cầu tâm A, cắt Δ tại hai điểm B và C sao cho BC = 8 là:
