Thực hiện các phép tính sau: \[\frac{3}{8} + \frac{5}{{24}}\]. Với kết quả là phân số tối giản
A. \[\frac{{14}}{{28}}\]
B. \[\frac{7}{{12}}\]
C. \[\frac{{112}}{{192}}\]
D. \[\frac{{12}}{7}\]
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có BCNN (8; 24) = 24 nên:
\[\frac{3}{8} + \frac{5}{{24}} = \frac{{3.3}}{{8.3}} + \frac{5}{{24}} = \frac{9}{{24}} + \frac{5}{{24}} = \frac{{14}}{{24}} = \frac{7}{{12}}\]
Đáp án cần chọn là: B
Một trường tổ chức cho học sinh đi tham quan bằng ôtô. Nếu xếp 35 hay 40 học sinh lên một ô tô thì đều thấy thiếu mất 5 ghế ngồi. Tính số học sinh đi tam quan biết số lượng học sinh đó trong khoảng từ 800 đến 900 em.
Một số tự nhiên aa khi chia cho 7 dư 4; chia cho 9 dư 6. Tìm số dư khi chia a cho 63.
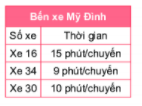
Lịch xuất bến của một số xe buýt tại bến xe Mỹ Đình (Hà Nội) được ghi ở bảng bên. Giả sử các xe buýt xuất bến cùng lúc vào 10 giờ 35 phút. Hỏi vào sau bao lâu thì cả 3 xe xuất bến cùng một lúc lần nữa (kể từ lần đầu tiên)?
Có bao nhiêu số có ba chữ số là bội chung của a và b, biết rằng
BCNN(a,b) = 300.
Cho tập hợp X là ước của 35 và lớn hơn 5. Cho tập Y là bội của 8 và nhỏ hơn 50. Gọi M là giao của 2 tập hợp X và Y, tập hợp M có bao nhiêu phần tử?
Cho a; b có BCNN(a; b) = 630; ƯCLN(a; b) = 18. Có bao nhiêu cặp số
a; b thỏa mãn?
Tìm hai số tự nhiên a, b(a < b). Biết a + b = 20, BCNN(a, b) = 15.
Tìm số tự nhiên n lớn nhất có 3 chữ số sao cho n chia 8 dư 7, chia 31 dư 28.
Tìm một số tự nhiên biết tích của ước số lớn nhất với bội số nhỏ nhất khác 0 của nó là 256.
Có bao nhiêu số tự nhiên x khác 0 thỏa mãn x∈BC(12;15;20) và x ≤ 100
Chị Hòa có một số bông sen. Nếu chị bó thành các bó gồm 3 bông, 5 bông hay 7 bông thì đều vừa hết. Hỏi chị Hòa có bao nhiêu bông sen? Biết rằng chị Hòa có khoảng từ 200 đến 300 bông.