Hàm số y = x – sin 2x đạt cực đại tại các điểm nào cho dưới đây?
A. x = -π/3 + kπ, k ∈ Z.
B. x = π/3 + kπ, k ∈ Z.
C. x = π/6 + kπ, k ∈ Z.
D. x = -π/6 + kπ, k ∈ Z.
Giải bởi Vietjack
Đáp án D.
Tập xác định: D = R
Ta có y’ = 1 – 2cos 2x
y’ = 0 ó 2x = ±π/3 + k2π ó x = ±π/6 + kπ, k ∈ Z
y’’ = 4sin 2x.
Khi đó:
y’’(π/6 + kπ) = 4sin(π/3 + k2π) = 2√3 > 0;
y’’(-π/6 + kπ) = 4sin(-π/3 + k2π) = -2√3
Vậy hàm số đạt cực đại tại x = - π/6 + kπ, k ∈ Z
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên:
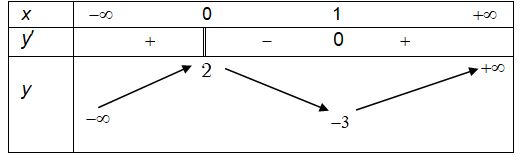
Khẳng định nào sau đây là khẳng định đúng?
Đồ thị hàm số y = ax3 + bx2 + cx + d có hai điểm cực trị A(0;0), B(1;1) thì các hệ số a, b, c, d có giá trị lần lượt là:
Tìm tất cả giá trị của m để hàm số y = 1/3.x3 – mx2 + (m2 – m + 1)x + 1 đạt cực đại tại x = 1
Khoảng cách giữa hai điểm cực đại và cực tiểu của đồ thị hàm số y = (x + 1)(x – 2)2
Đồ thị hàm số y = x4 – 3x2 + ax + b có điểm cực tiểu A(2;-2). Tính tổng (a + b)
Cho hàm số y = x3/3 – 2x2 + 3x + 2/3. Toạ độ điểm cực đại của đồ thị hàm số là
Hàm số y = x – sin 2x + 3. Chọn khẳng định đúng trong các khẳng định sau?
Đồ thị của hàm số y = 3x4 – 4x3 – 6x2 + 12x + 1 đạt cực tiểu tại M(x1; y1). Tính tổng x1 + y1
Cho hàm số y = -x3 + 3x2 – 3x + 1, mệnh đề nào sau đây là đúng?
