Trong mặt phẳng tọa độ Oxy, tìm tập hợp điểm biểu diễn các số phức z thỏa mãn |z-i| = |(1+i)z|
A. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(2;=1) bán kính R =
B. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0;1) bán kính R =
C. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0;-1) bán kính R =
D. Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0;-1)bán kính R =
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Đặt z = x + yi, ta có:
![]()
![]()
![]()
![]()
![]()
![]()
Vậy tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I(0;-1)bán kính R =
Gọi số phức z = a + bi(a,b) thỏa mãn |z-1| = 1 và (1+i)(-1) có phần thực bằng 1 đồng thời z không là số thực. Khi đó a.b bằng
Cho hai số phức , thỏa mãn || = || = |-| = 1. Tính giá trị của biểu thức P =
Cho số phức thỏa mãn |z| 1. Đặt A = . Mệnh đề nào sau đây đúng?
Trong mặt phẳng phức, gọi M là điểm biểu diễn số phức với z = a + bi(a,b). Chọn kết luận đúng.
Gọi , là hai nghiệm phức của phương trình + 2z + 10 = 0. Tính giá trị của biểu thức A =
Gọi là hai nghiệm của phương trình - 2z + 2 = 0. Tính giá trị của biểu thức P =
Cho số phức z thỏa mãn (3-4i)z - = 8. Trên mặt phẳng tọa độ, khoảng cách từ gốc tọa độ đến điểm biểu diễn số phức z thuộc tập nào?
Cho số phức z thỏa mãn z(2-i) + 13i = 1. Tính mô đun của số phức z.
Cho số phức z có phần ảo âm, gọi w = 2z + |z-|i. Khi đó khẳng định nào sau đây về w là đúng?
Cho A, B, C là những điểm biểu diễn các số phức thỏa mãn + i = 0. Tìm phát biểu sai?
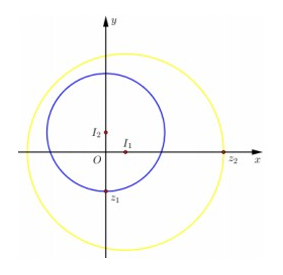
Gọi T là tập hợp các số phức z thỏa mãn |z-i|3 và |z-i|5. Gọi lần lượt là các số phức có môđun nhỏ nhất và lớn nhất. Tìm số phức
Tập hợp các điểm biểu diễn số phức z thỏa mãn 2|z-1| = |z + +2| trên mặt phẳng tọa độ là một
Cho số phức z thỏa mãn |z - 3 - 4i| = . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = . Tính môđun của số phức w = M + mi ?