Tìm phần thực phần ảo của số phức z thỏa mãn điều kiện sau: (2+3i)z = z - 1
B. Phần thực a = - phần ảo b =
B. Phần thực a = phần ảo b = -
C. Phần thực a = - phần ảo b = i
D. Phần thực a = phần ảo b =
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A.
![]()
![]()
Gọi là hai nghiệm phức của phương trình - 2z + 2 = 0. Khi đó giá trị biểu thức A = bằng:
Gọi z1, z2 là hai nghiệm của phương trình + z + 1 = 0. Tính giá trị của biểu thức ?
Cho số phức z thay đổi hoàn toàn thỏa mãn: |z-i| = |z-1+2i|. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn: w = (2-i)z+1 là một đường thẳng. Viết phương trình đường thẳng đó.
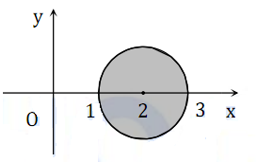
Biết các số phức z có tập hợp điểm trên mặt phẳng tọa độ là hình tròn tô đậm như hình vẽ. Modul lớn nhất của số phức z là:
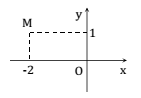
Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm M như hình bên?
Trong mặt phẳng phức cho điểm . Trong các khẳng định sau, khẳng định nào sai?
Cho số phức z thỏa mãn điều kiện (z+2)(1+2i) = 5. Tìm phần ảo của số phức w =
Cho số phức z thỏa mãn: |z+2+i| = 4. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của |z-1-2i|. Tính S = M + m.
Tìm tổng các giá trị của m để hai phương trình + mz + 2 = 0 và - + 2z + m có ít nhất một nghiệm phức chung.
Cho số phức z thỏa mãn |z+i| = 1. Biết rằng tập hợp các điểm biểu diễn các số phức w = z - 2i là một đường tròn. Tâm của đường tròn đó là:
Gọi z1, z2, z3 và z4 là bốn nghiệm phức của phương trình - 12 = 0. Tính tổng T = |z1| + |z2| + |z3| + |z4|