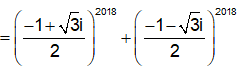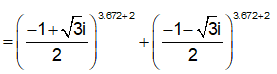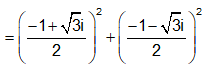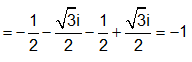225 Bài tập Số phức ôn thi Đại học có lời giải (P7)
-
6017 lượt thi
-
25 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho số phức z thỏa mãn: |z+2+i| = 4. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của |z-1-2i|. Tính S = M + m.
 Xem đáp án
Xem đáp án
Đáp án A
Em có: ![]()
![]()
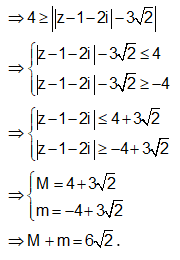
Câu 2:
Cho số phức z thỏa mãn |z+2i+3| = |-i|. Tìm giá trị nhỏ nhất của |z|.
 Xem đáp án
Xem đáp án
Đáp án A
Gọi: ![]()
Em có:
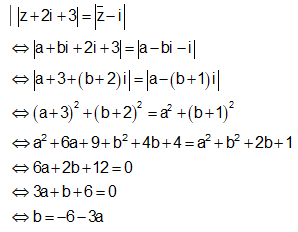
![]()
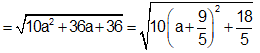
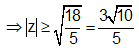
Câu 3:
Cho số phức z thay đổi hoàn toàn thỏa mãn: |z-i| = |z-1+2i|. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn: w = (2-i)z+1 là một đường thẳng. Viết phương trình đường thẳng đó.
 Xem đáp án
Xem đáp án
Đáp án C
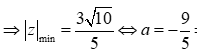
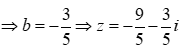
Đặt ![]()
Đặt ![]() Số phức w được biểu diễn bởi điểm M(x';y')
Số phức w được biểu diễn bởi điểm M(x';y')
Em có:
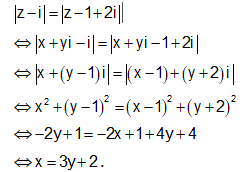
Em có: ![]()
![]()
Mà x = 3y + 2 nên w = ![]()
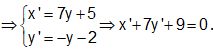
Vậy số phức w được biểu diễn bởi đoạn thẳng: x + 7y + 9 = 0
Câu 4:
Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm M như hình bên?
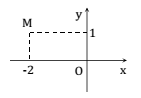
 Xem đáp án
Xem đáp án
Đáp án C
Từ hình vẽ ta thấy M có tọa độ M(-2;1)
M là điểm biểu diễn của số phức z = -2 + i
Câu 5:
Tìm tổng các giá trị của m để hai phương trình + mz + 2 = 0 và - + 2z + m có ít nhất một nghiệm phức chung.
 Xem đáp án
Xem đáp án
Đáp án C
Giả sử hai phương trình đã cho có nghiệm phức chung khi đó ta có hệ phương trình:
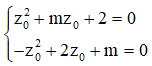
![]()
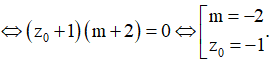
TH1: Nếu m = -2 thì khi đó 2 phương trình trở thành: - 2z + 2 trùng nhau nên có nghiệm chung.
TH2: Nếu = -1 thay vào hệ ta được:
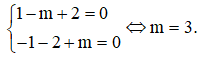
Vậy giá trị cần tìm là m = -2 và m = 3.
Câu 6:
Cho số phức z thỏa mãn điều kiện (z+2)(1+2i) = 5. Tìm phần ảo của số phức w =
 Xem đáp án
Xem đáp án
Đáp án A
Đặt z = x + yi với x,y , ta có:
![]()
![]()
![]() = 5x - 5yi
= 5x - 5yi
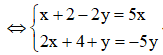
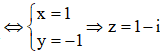
Do đó ![]()
![]()
Vậy w có phần ảo bằng
Câu 7:
Cho số phức z thỏa mãn: |z-3-2i| = 1. Tìm giá trị nhỏ nhất của |-1-i|
 Xem đáp án
Xem đáp án
Đáp án B
Gọi: ![]()
Ta có:
![]()
![]()
![]()
![]()
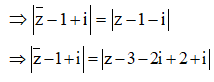
![]()
![]()
=> Giá trị nhỏ nhất của -1-i| là - 1
Câu 8:
Cho số phức z thỏa mãn: |z|= 4. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn: w = (3+4i)z + i là một đường tròn có bán kính là:
 Xem đáp án
Xem đáp án
Đáp án C
Đặt ![]() Số phức w được biểu diễn bởi điểm M (x;y).
Số phức w được biểu diễn bởi điểm M (x;y).
Ta có:
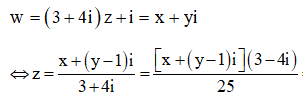
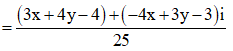
=> |z| = 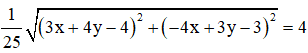
![]()
![]()
![]()
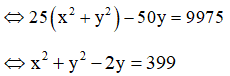
![]()
Vậy số phức w được biểu diễn bởi đường tròn tâm I (0;1), bán kính R = 20 và có phương trình: ![]()
Câu 9:
Tính môđun của số phức z biết = (4-3i)(1+i).
 Xem đáp án
Xem đáp án
Đáp án C
Cách 1: Áp dụng quy tắc nhân, em tính được
![]()
![]()
![]()
Cách 2:
Áp dụng công thức giải nhanh: ![]()
![]()
![]()
= 5
Em ấn MODE 2 SHIFT hyp (để tính mô đun) nhập (4-3i)(1+i) =
Em được kết quả là 5
Câu 10:
Kết quả của phép tính: P = 1 + i + ..... +
 Xem đáp án
Xem đáp án
Đáp án C
Em thấy trong biểu thức P gồm bao nhiêu số hạng và các số hạng có quan hệ gì?
P có 2018 số hạng. Nếu em tính riêng mỗi số hạng ik với k = 1,2,...., 2016,2017 thì việc cộng các kết quả đó cũng không đơn giản chút nào.
Kể từ số hạng thứ hai, số hạng sau gấp số hạng đứng ngay trước nó là i. Vậy nên P là tổng của 2018 số hạng đầu của một cấp số nhân, với số hạng đầu là = 1 và công bội q = i. Sử dụng công thức tính tổng của n số hạng đầu của cấp số nhân với số hạng dầu và công bội q:
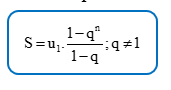
![]()
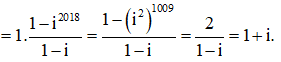
Câu 11:
Mệnh đề nào sau đây đúng.
 Xem đáp án
Xem đáp án
Đáp án D
Kiểm tra từ đáp án đơn giản đến phức tạp em thấy:
Đặt ![]() nên
nên ![]()
Câu 12:
Cho số phức z thỏa mãn điều kiện: |z-1| = |z+3-2i|. Tập hợp các điểm biểu diễn số phức z là
 Xem đáp án
Xem đáp án
Đáp án A
Em hãy thực hiện Câu nay theo cả 2 cách nhé!
Cách 1: Đặt ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Cách 2: ![]() với M(x;y), A(1;0) và B(-3;2)
với M(x;y), A(1;0) và B(-3;2)
Em thấy, điểm M cách đều hai điểm A, B nên M thuộc đường trung trực của đoạn thẳng AB.
Em có thể tìm phương trình đường trung trực của đoạn thẳng AB như sau:
![]() trung điểm của AB là I(-1;1), qua điểm I nhận
trung điểm của AB là I(-1;1), qua điểm I nhận ![]() làm vectơ pháp tuyến.
làm vectơ pháp tuyến.
![]()
![]()
Câu 13:
Gọi z1, z2, z3 và z4 là bốn nghiệm phức của phương trình - 12 = 0. Tính tổng T = |z1| + |z2| + |z3| + |z4|
 Xem đáp án
Xem đáp án
Đáp án C
![]()
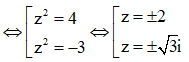
![]()
![]()
![]()
Câu 14:
Tìm phần thực phần ảo của số phức z thỏa mãn điều kiện sau: (2+3i)z = z - 1
 Xem đáp án
Xem đáp án
Đáp án A.
![]()
![]()
Câu 15:
Cho hai số phức z = (2x+3) + (3y-1)i và z' = (y-1)i. Ta có z = z' khi:
 Xem đáp án
Xem đáp án
Đáp án B.
Ta có z = z'
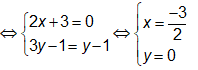
Câu 16:
Tìm tham số m để số phức z = m(-5) - mi là số thuần ảo.
 Xem đáp án
Xem đáp án
Đáp án C.
Ta có z = m(-5) - mi
Để z là số thuần ảo thì
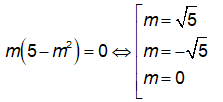
Câu 17:
Trong mặt phẳng phức cho điểm . Trong các khẳng định sau, khẳng định nào sai?
 Xem đáp án
Xem đáp án
Đáp án B.
Ta có ![]() nên A, C đúng; số phức có phần thực bằng . Nên B SAI.
nên A, C đúng; số phức có phần thực bằng . Nên B SAI.
Câu 18:
Gọi là hai nghiệm phức của phương trình - 2z + 2 = 0. Khi đó giá trị biểu thức A = bằng:
 Xem đáp án
Xem đáp án
Đáp án A.
Biệt số ![]()
Do đó phương trình có 2 nghiệm phức là: 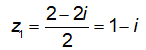 và
và 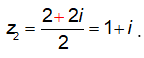
Suy ra
![]()
![]()
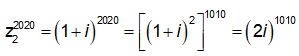
![]()
Vậy ![]()
Câu 19:
Cho số phức z thỏa mãn |z+i| = 1. Biết rằng tập hợp các điểm biểu diễn các số phức w = z - 2i là một đường tròn. Tâm của đường tròn đó là:
 Xem đáp án
Xem đáp án
Đáp án B.
Ta có ![]()
Gọi ![]() Suy ra z = x + (2+y).i
Suy ra z = x + (2+y).i
Suy ra
Theo giả thiết, ta có ![]()
![]()
![]()
Vậy tập hợp các số phức w = z - 2i là đường tròn tâm I(0;-3).
Câu 21:
Phương trình: - 6(z + 3 - i) + 13 = 0 có 2 nghiệm phân biệt. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án C
Em có:
![]()
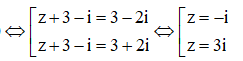
Câu 22:
Cho số phức z thỏa mãn |z + 2 - i| + |z - 5 + 6i| = 7. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = |z - 1 + 2i|. Tổng M + m là:
 Xem đáp án
Xem đáp án
Đáp án C
Đặt ![]() Số phức z được biểu diễn bởi điểm N(x;y)
Số phức z được biểu diễn bởi điểm N(x;y)
Số phức ![]() được biểu diễn bởi điểm A(-2;1)
được biểu diễn bởi điểm A(-2;1)
Số phức ![]() được biểu diễn bởi điểm B(5;-6)
được biểu diễn bởi điểm B(5;-6)
được biểu diễn bởi điểm
Ta có: |z + 2 - i| + |z - 5 + 6i| = 7![]() Mà AB = 7 nên N thuộc đoạn thẳng AB.
Mà AB = 7 nên N thuộc đoạn thẳng AB.
Đường thẳng AB: 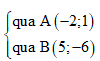
=> phương trình đường thẳng AB là: x + y + 1 = 0
Vì N(x;y) thuộc đoạn thẳng AB nên x + y +1 = 0, x[-2;5]
Ta có: ![]()
![]()
![]()
![]()
Xét ![]() trên [-2;5] ta có: f'(x) = 4(x-1)
trên [-2;5] ta có: f'(x) = 4(x-1)
![]()
Ta có:
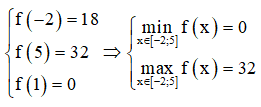
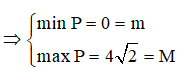
Vậy M + m = 4
Câu 23:
Biết các số phức z có tập hợp điểm trên mặt phẳng tọa độ là hình tròn tô đậm như hình vẽ. Modul lớn nhất của số phức z là:
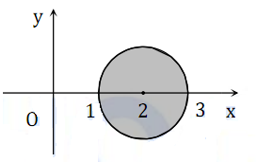
 Xem đáp án
Xem đáp án
Đáp án C
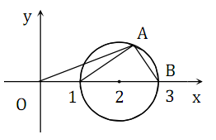
Giả sử A là điểm biểu diễn của số phức z trên mặt phẳng toạn độ, B(3;0).
Tam giác OAB có góc OAB là góc tù nên OAOB => z OB = 3
Do đó = 3
Câu 24:
Cho số phức z thỏa mãn: |z-3-4i| = 1. Tìm giá trị lớn nhất của |z|
 Xem đáp án
Xem đáp án
Đáp án C
Em có: 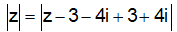
![]()
![]()
=> Giá trị lớn nhất của |z| là 6
Câu 25:
Gọi z1, z2 là hai nghiệm của phương trình + z + 1 = 0. Tính giá trị của biểu thức ?
 Xem đáp án
Xem đáp án
Đáp án D
Cách 1: Em có z = 1 không là nghiệm của phương trình trên.
![]()
![]()
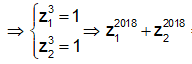
![]()
![]()
Theo định lý Vi-ét em có
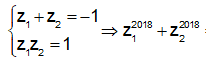
![]()
Cách 2: Em có
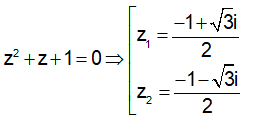
![]()