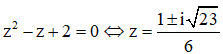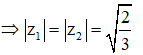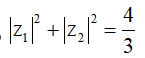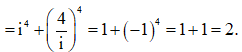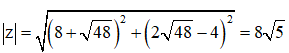225 Bài tập Số phức ôn thi Đại học có lời giải (P3)
-
6107 lượt thi
-
25 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho hai số phức z, w khác 0 và thỏa mãn biết |w| = 1. Mệnh đề nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án C.
Từ giả thiết, ta có 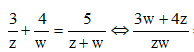
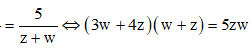
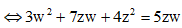
![]()

![]()
Lấy modun hai vế, ta được
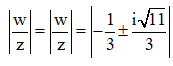
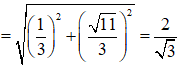
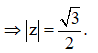
Câu 2:
Tìm phần thực và phần ảo của số phức z, biết
 Xem đáp án
Xem đáp án
Đáp án C
Ta có ![]()
![]()
Do đó số phức z có phần thực bằng 14 và phần ảo bằng
Câu 4:
Cho số phức z = a + bi(a,b). Biết tập hợp các điểm A biểu diễn hình học số phức z là đường tròn (C) có tâm I(4;3) và bán kính R = 3. Đặt M là giá trị lớn nhất, m là giá trị nhỏ nhất của F = 4a + 3b - 1. Tính giá trị M + m
 Xem đáp án
Xem đáp án
Đáp án B
Theo đề ta có 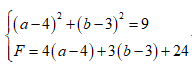
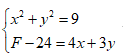
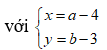
![]()
![]()
![]()
![]()
Câu 5:
Biết rằng phương trình + bz + c = 0(b,c) có một nghiệm phức là = 1 + 2i. Khi đó
 Xem đáp án
Xem đáp án
Đáp án B
Do 1 + 2i là nghiệm của phương trình nên ta có:

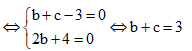
Câu 6:
Cho số phức z thay đổi, luôn có |z| = 2. Khi đó tập hợp điểm biểu diễn số phức w = (1-2i) + 3i là:
 Xem đáp án
Xem đáp án
Đáp án C
Giả sử ![]()
![]()
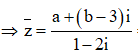
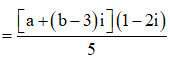
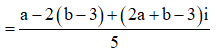
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Câu 7:
Cho số phức z, w khác 0 sao cho |z-w| = 2|z| = |w|. Phần thực của số phức là
 Xem đáp án
Xem đáp án
Đáp án D
Giả sử ![]()
Từ giả thiết đầu bài |z-w| = 2|z| = |w|, ta có hệ sau
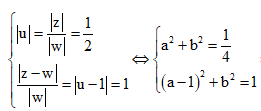
![]()
Câu 8:
Cho số phức z thỏa . Tìm
 Xem đáp án
Xem đáp án
Đáp án C
Giả thiết 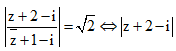
![]()
![]()
![]()
![]()
Đặt ![]()
![]() khi đó
khi đó
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
=> Do đó tập hợp điểm biễu diễn z là đường tròn tâm I(0;-3), bán kính R =
![]()
![]()
Câu 10:
Tìm tập hợp điểm biểu diễn số phức z thỏa mãn |z+2-i| = 3
 Xem đáp án
Xem đáp án
Đáp án D
Đặt ![]() khi đó
khi đó ![]()
![]()
Do đó tập hợp điểm biễu diễn z là đường tròn tâm I(-2;1) bán kính R = 3
Câu 11:
Cho số phức z thỏa mãn |z| = + 2m, trong đó m là số thực dương tùy ý. Biết rằng với mỗi m, tập hợp các điểm biểu diễn số phức w = (2i+1)(i+)-5+3i là một đường tròn bán kính r. Tìm giá trị nhỏ nhất của r
 Xem đáp án
Xem đáp án
Đáp án C
Ta có ![]()
![]()
![]()
![]()
![]()
![]()
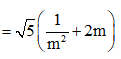
theo bất đẳng thức AM-GM, ta có
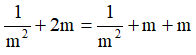
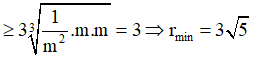
Câu 12:
Cho hai số phức = 4 - i, = -2 + 3i. Tìm phần ảo của số phức
 Xem đáp án
Xem đáp án
Đáp án B.
Ta có
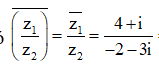
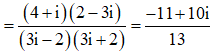
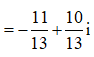
=> phần ảo của số phức là
Câu 13:
Giả sử là hai trong số các số phức z thỏa mãn |iz + - i| = 1 và || = 2. Giá trị lớn nhất của || + || bằng
 Xem đáp án
Xem đáp án
Đáp án D.
Ta có: ![]()
![]()
![]()
=> M(x;y) biểu diễn z thuộc đường tròn tâm I(1;) bán kính R = 1
Giả sử ![]() => AB = 2 = 2R nên B là đường kính của đường tròn (I;R)
=> AB = 2 = 2R nên B là đường kính của đường tròn (I;R)
Lại có: || + || = OA + OB
Mặt khác theo công thức trung tuyến ta có:
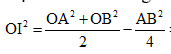
![]()
Theo BĐT Bunhiascopky ta có: ![]()
![]()
Câu 15:
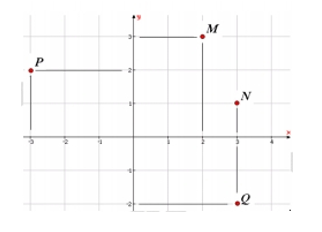
Cho số phức z = 3 + 2i. Điểm nào trong các điểm M, N, P, Q hình bên là điểm biểu diễn số phức liên hợp của z?
 Xem đáp án
Xem đáp án
Đáp án D.
![]()
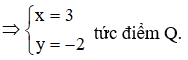
Câu 16:
Có bao nhiêu số phức z thỏa mãn
 Xem đáp án
Xem đáp án
Đáp án C.
Giả sử ![]()
![]()
![]()
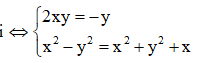
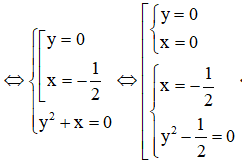
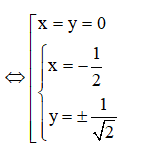
Do đó có 3 số phức z thỏa mãn bài toán.
Câu 18:
Tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện |z-(1+i)| = |z+2i| là đường nào trong các đường cho dưới đây?
 Xem đáp án
Xem đáp án
Đáp án A
Giả sử z = x + yi
Ta có ![]()
![]()
![]()
Tập hợp các điểm biểu diễn số phức z thỏa mãn điều kiện |z-(1+i)| = |z+2i| là đường thẳng
Câu 19:
Cho số phức z thỏa mãn = 9 - 3i. Gọi M là điểm biểu diễn số phức z. Tìm tung độ của M
 Xem đáp án
Xem đáp án
Đáp án C
Ta có 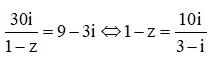
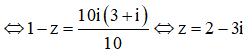
Câu 21:
Tìm tất cả các điểm trong mặt phẳng biểu diễn số phức z thỏa mãn điều kiện 2 z là một số thực âm
 Xem đáp án
Xem đáp án
Đáp án C
Giả sử ![]()
Ta có ![]()
Để là một số thực âm thì 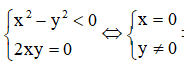
=> biểu diễn là trục tung (trừ gốc tọa độ O)
Câu 22:
Cho số phức z thỏa mãn điều kiện |z| = 1. Tìm giá trị lớn nhất của A = |1+z| +3|1-z|
 Xem đáp án
Xem đáp án
Đáp án D
Đặt ![]()
Khi đó ![]()
![]()
Xét hàm số ![]()
![]()
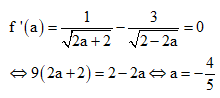
Khi đó ![]()
Câu 23:
Cho là hai nghiệm của phương trình - 2016z + 2017 = 0. Tính giá trị của biểu thức P =
 Xem đáp án
Xem đáp án
Đáp án D
![]()
![]()
![]()
![]()
![]()
![]()
Dễ thấy ![]() suy ra
suy ra ![]()
Câu 24:
Cho số phức z = a + bi(a,b ) thỏa điều kiện (2-3i)z - 7i. = 22-20i. Tính a+b
 Xem đáp án
Xem đáp án
Đáp án B.
Ta có ![]()
![]()
![]()
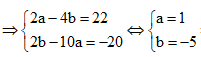
![]()
Câu 25:
Có bao nhiêu số phức z thỏa mãn |z| = = 1?
 Xem đáp án
Xem đáp án
Đáp án C.
Đặt z = a + bi với ![]()
![]()
Ta có: 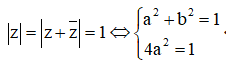
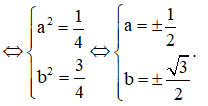
Vậy có tất cả 4 số phức thảo mãn.