Đề kiểm tra 15 phút có 10 câu trắc nghiệm, mỗi câu có bốn phương án trả lời, trong đó có một phương án đúng, mỗi câu trả lời đúng được 1,0 điểm. Một thí sinh làm cả 10 câu, mỗi câu chọn một phương án. Tính xác suất để thí sinh đó đạt từ 8,0 điểm trở lên.
Giải bởi Vietjack
Chọn A
Cách 1: Vì mỗi câu hỏi có bốn phương án trả lời và chỉ có một phương án đúng nên xác suất để trả lời đúng và xác suất để trả lời sai một câu hỏi lần lượt là
Theo yêu cầu của bài toán có các trường hợp sau:
|
Trường hợp |
Số câu trả lời đúng |
Số câu trả lời sai |
Xác suất xảy ra |
|
TH1 |
8 |
2 |
(quy tắc nhân) |
|
TH2 |
9 |
1 |
(quy tắc nhân) |
|
TH3 |
10 |
0 |
(quy tắc nhân) |
Vậy áp dụng quy tắc cộng ta có xác suất cần tìm là:
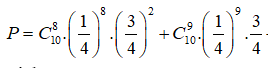
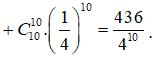
Cách 2:
- Số cách làm bài của thí sinh: (cách).
- Để thí sinh đó đạt từ 8,0 điểm trở lên, ta có 3 trường hợp sau:
+ Làm được 8 câu đúng và 2 câu sai (8 điểm): 
+ Làm được 9 câu đúng và 1 câu sai (9 điểm): 
+ Làm được 10 câu đúng (10 điểm): 1 (cách).
Do đó số cách để thí sinh đạt từ 8,0 điểm trở lên là: 
Vậy xác suất cần tìm là 
Có tất cả 120 cách chọn 3 học sinh từ nhóm n(chưa biết) học sinh. Số n là nghiệm của phương trình nào sau đây?
Cho đa giác đều có 20 cạnh. Có bao nhiêu hình chữ nhật (không phải là hình vuông), có các đỉnh là đỉnh của đa giác đều đã cho?
Có bao nhiêu cách chia hết 4 chiếc bánh khác nhau cho 3 em nhỏ, biết rằng mỗi em nhận được ít nhất 1 chiếc.
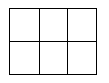
Bé Minh có một bảng hình chữ nhật gồm 6 hình vuông đơn vị, cố định không xoay như hình vẽ. Bé muốn dùng 3 màu để tô tất cả các cạnh của các hình vuông đơn vị, mỗi cạnh tô một lần sao cho hình vuông đơn vị được tô bởi đúng 2 màu, trong đó mỗi màu tô đúng hai cạnh. Hỏi bé Minh có tất cả bao nhiêu cách tô màu bảng?
Với k, n là hai số nguyên dương tùy ý thỏa mãn k ≤ n-1, mệnh đề nào dưới đây sai?
Cho tứ giác ABCD. Trên các cạnh AB, BC, CD, AD lần lượt lấy 3;4;5;6 điểm phân biệt khác các điểm A, B, C, D. Số tam giác phân biệt có các đỉnh là các điểm vừa lấy là
Tổ 1 gồm 10 bạn học sinh. Có bao nhiêu cách để cô giáo chủ nhiệm chọn ra 4 em đi bưng bàn ghế?
Có bao nhiêu cách bỏ đồng thời 7 quả bóng bàn giống nhau vào 4 hộp khác nhau sao cho mỗi hộp có ít nhất 1 quả?
Số tập con gồm nhiều nhất 3 phần tử của tập A = {1,2,....,10} là
Cho k, n là số nguyên dương thỏa mãn 1k n. Đẳng thức nào sau đây đúng?
Một tập hợp M có tập con. Hỏi M có bao nhiêu tập con có ít nhất 2017 phần tử?
Đội văn nghệ của trường THPT Hùng Vương có 9 học sinh, trong đó có 4 học sinh lớp 12, 3 học sinh lớp 11 và 2 học sinh lớp 10. Hỏi có bao nhiêu cách chọn ra một nhóm có ít nhất 3 học sinh để biểu diễn dịp 26 tháng 3 sao cho mỗi khối có ít nhất một học sinh, biết rằng năng khiếu văn nghệ của các em là như nhau
