Cho \(\Delta ABC\) (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) bằng một tam giác có ba đỉnh là T, S, R. Viết kí hiệu về sự bằng nhau của hai tam giác, biết rằng \(\widehat A = \widehat T\), AC = TS.
Giải bởi Vietjack
Đáp án đúng là: A
Ta có:
\(\widehat A = \widehat T\) ⇒ A, T là hai đỉnh tương ứng.
AC = TS ⇒ C, S là hai đỉnh tương ứng.
Do đó B, R là hai đỉnh tương ứng.
\( \Rightarrow \)\[\Delta ABC = \Delta TRS\].
Cho hai tam giác \[\Delta ABC\] và \[\Delta DEF\] có: AB = EF, BC = FD, AC = ED và \[\widehat A = \widehat E\]; \[\widehat B = \widehat F\]; \[\widehat D = \widehat C\]. Cách viết nào dưới đây đúng?
Cho hình vẽ dưới đây, biết JG = JL, GK = LK, \(\widehat {KJL} = 60^\circ \), \(\widehat {JGK} = 90^\circ \).
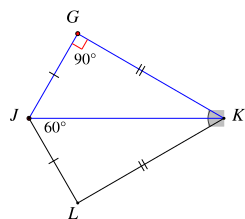
Số đo góc GKL là
Cho \(\Delta ABC = \Delta DEF\). Biết \(\widehat A + \widehat B = 140^\circ \), \(\widehat E = 45^\circ \). Tính góc A, C, D, F.
Cho \[\Delta ABC = \Delta MNP\] biết AC = 5 cm. Cạnh nào của \[\Delta MNP\]có độ dài bằng 5 cm?
Cho \(\Delta {\rm{PQR}} = \Delta {\rm{DEF}}\). Biết \(\widehat P = 33^\circ \). Khi đó:
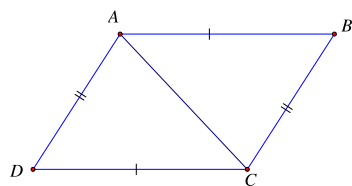
Cho hình vẽ dưới đây, biết AB = CD; AD = BC. Góc có số đo bằng góc ABC là
Cho \[\Delta ABC = \Delta MNP\] có AB = 2 cm; AC = 3 cm; PN = 4 cm. Chu vi \[\Delta MNP\] là
Cho \[\Delta ABC = \Delta MNP\] biết \[\widehat A = 40^\circ \] và \[\widehat B = 70^\circ \]. Số đo \[\widehat P\] bằng
Cho \[\Delta ABC = \Delta MNP\]. Biết AB = 5 cm, MP = 7 cm và chu vi của \(\Delta ABC\) là 22 cm. Tính cạnh NP và BC.
