Trắc nghiệm Bài 13. Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của hai tam giác có đáp án
Trắc nghiệm Bài 13. Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của hai tam giác có đáp án
-
467 lượt thi
-
14 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho \[\Delta ABC = \Delta MNP\]. Khẳng định nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Vì \[\Delta ABC = \Delta MNP\] nên:
\(\widehat A = \widehat M\); \(\widehat B = \widehat N\); \(\widehat C = \widehat P\) (các góc tương ứng bằng nhau)
AB = MN; BC = NP; AC = MP (các cạnh tương ứng bằng nhau)
Vậy \[\widehat {ABC} = \widehat {MNP}\] là khẳng định đúng.
Câu 2:
Cho \(\Delta {\rm{PQR}} = \Delta {\rm{DEF}}\). Biết \(\widehat P = 33^\circ \). Khi đó:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Vì \(\Delta {\rm{PQR}} = \Delta {\rm{DEF}}\)
⇒ \(\widehat D = \widehat P\) (hai góc tương ứng bằng nhau)
Nên \[\widehat D = 33^\circ \].
Câu 3:
Cho hai tam giác \[\Delta ABC\] và \[\Delta DEF\] có: AB = EF, BC = FD, AC = ED và \[\widehat A = \widehat E\]; \[\widehat B = \widehat F\]; \[\widehat D = \widehat C\]. Cách viết nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét \[\Delta ABC\] và \[\Delta DEF\] có:
AB = EF, BC = FD, AC = ED (các cạnh tương ứng bằng nhau)
và \[\widehat A = \widehat E\]; \[\widehat B = \widehat F\]; \[\widehat D = \widehat C\] (các góc tương ứng bằng nhau).
⇒ \[\Delta ABC = \Delta EFD\]
Câu 4:
Cho \[\Delta ABC = \Delta MNP\] có AB = 2 cm; AC = 3 cm; PN = 4 cm. Chu vi \[\Delta MNP\] là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì \[\Delta MNP = \Delta ABC\] nên
MN = AB = 2 cm; MP = AC = 3 cm (cách cạnh tương ứng bằng nhau)
Chu vi \[\Delta MNP\] là: MN + MP + PN = 2 + 3 + 4 = 9 (cm)
Câu 5:
Cho \[\Delta ABC = \Delta MNP\] biết \[\widehat A = 40^\circ \] và \[\widehat B = 70^\circ \]. Số đo \[\widehat P\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Vì \[\Delta MNP = \Delta ABC\] nên
\[\widehat M = \widehat A = 40^\circ \]; \[\widehat N = \widehat B = 70^\circ \] (các góc tương ứng bằng nhau)
Xét \(\Delta MNP\) có \(\widehat M + \widehat N + \widehat P = 180^\circ \) (tổng ba góc của một tam giác)
⇒ \(\widehat P = 180^\circ - \left( {\widehat M + \widehat N} \right) = 180^\circ - \left( {40^\circ + 70^\circ } \right) = 70^\circ \).
Vậy \(\widehat P = 70^\circ \).
Câu 6:
Cho \[\Delta ABC = \Delta MNP\]. Biết AB = 5 cm, MP = 7 cm và chu vi của \(\Delta ABC\) là 22 cm. Tính cạnh NP và BC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì \[\Delta ABC = \Delta MNP\] nên
AC = MP = 7 cm (hai cạnh tương ứng bằng nhau)
BC = NP (hai cạnh tương ứng bằng nhau)
Chu vi của \(\Delta ABC\) là: AB + AC + BC = 22 (cm)
⇒ 5 + 7 + BC = 22
⇒ BC = 10 (cm)
Mà NP = BC (chứng minh trên)
⇒ NP = BC = 10 cm
Câu 7:
Cho \[\Delta ABC = \Delta MNP\] biết AC = 5 cm. Cạnh nào của \[\Delta MNP\]có độ dài bằng 5 cm?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì \[\Delta ABC = \Delta MNP\] nên
AC = MP (hai cạnh tương ứng bằng nhau)
Mà AC = 5 cm
Nên MP = 5 cm
Câu 8:
Cho \(\Delta ABC\) (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) bằng một tam giác có ba đỉnh là T, S, R. Viết kí hiệu về sự bằng nhau của hai tam giác, biết rằng \(\widehat A = \widehat T\), AC = TS.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có:
\(\widehat A = \widehat T\) ⇒ A, T là hai đỉnh tương ứng.
AC = TS ⇒ C, S là hai đỉnh tương ứng.
Do đó B, R là hai đỉnh tương ứng.
\( \Rightarrow \)\[\Delta ABC = \Delta TRS\].
Câu 9:
Cho \(\Delta ABC = \Delta DEF\). Biết \(\widehat A + \widehat B = 140^\circ \), \(\widehat E = 45^\circ \). Tính góc A, C, D, F.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì \(\Delta ABC = \Delta DEF\) nên
\(\widehat A = \widehat D\), \(\widehat C = \widehat F\), \(\widehat B = \widehat E = 45^\circ \) (các góc tương ứng bằng nhau).
Xét \(\Delta ABC\) ta có \(\widehat A + \widehat B = 140^\circ \).
⇒ \(\widehat A = 140^\circ - \widehat B = 140^\circ - 45^\circ = 95^\circ \)
Lại có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng ba góc của một tam giác)
⇒ \(\widehat C = 180^\circ - (\widehat A + \widehat B)\)
⇒ \(\widehat C = 180^\circ - 140^\circ = 40^\circ \).\(\)
⇒ \(\widehat F = \widehat C = 40^\circ \)
Vậy \[\widehat A = \widehat D = 95^\circ \], \[\,\widehat F = \widehat C = 40^\circ \]
Câu 10:
Cho tam giác ABC và DEH trong hình dưới đây.
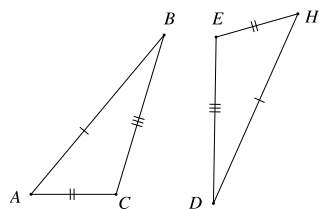
Khẳng định đúng là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Hai tam giác ABC và DEH có:
AB = HD
BC = DE
AC = HE
(Khi đó A và H (B và D; C và E) là hai đỉnh tương ứng)
Vậy \(\Delta ABC = \Delta HDE\)(c.c.c)
Câu 11:
Cho hình vẽ dưới đây, biết AD = BC, AC = BD. Khẳng định đúng là
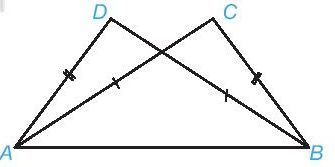
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Hai tam giác ADB và BCA có:
AD = BC (theo giả thiết)
BD = AC (theo giả thiết)
AB là cạnh chung
Vậy \(\Delta ADB = \Delta BCA\) (c.c.c)
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Trường hợp bằng nhau cạnh - cạnh - cạnh (c.c.c)
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
Câu 13:
Cho hình vẽ dưới đây, biết AB = CD; AD = BC. Góc có số đo bằng góc ABC là
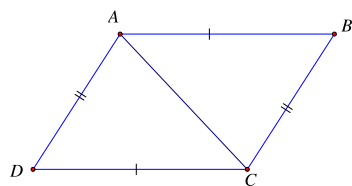
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Xét hai tam giác ABC và CDA có:
AB = CD (theo giả thiết)
BC = AD (theo giả thiết)
AC là cạnh chung
Vậy \(\Delta ABC = \Delta CDA\) (c.c.c)
⇒ \(\widehat {ABC} = \widehat {CDA}\)(hai góc tương ứng)
Câu 14:
Cho hình vẽ dưới đây, biết JG = JL, GK = LK, \(\widehat {KJL} = 60^\circ \), \(\widehat {JGK} = 90^\circ \).
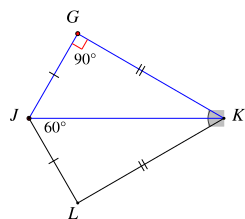
Số đo góc GKL là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét hai tam giác JGK và JLK có:
JG = JL (theo giả thiết)
GK = LK (theo giả thiết)
JK là cạnh chung
Vậy \(\Delta JGK = \Delta JLK\) (c.c.c)
⇒ \(\widehat {KJG} = \widehat {KJL}\)(hai góc tương ứng)
⇒ \(\widehat {KJG} = 60^\circ \)
Xét tam giác JGK có: \(\widehat {KJG} + \widehat {JGK} + \widehat {GKJ} = 180^\circ \) (tổng 3 góc trong tam giác)
⇒ \(60^\circ + 90^\circ + \widehat {GKJ} = 180^\circ \)
⇒ \(\widehat {GKJ} = 180^\circ - 60^\circ - 90^\circ = 30^\circ \)
Vì\(\Delta JGK = \Delta JLK\) (theo câu a)
⇒ \(\widehat {GKJ} = \widehat {LKJ}\)(hai góc tương ứng)
⇒ \(\widehat {GKL} = \widehat {GKJ} + \widehat {LKJ} = \widehat {GKJ} + \widehat {GKJ} = 2\widehat {GKJ} = 2 \cdot 30^\circ = 60^\circ \)
Vậy \(\widehat {GKL} = 60^\circ \).
