Cho tứ diện ABCD có tất cả các cạnh đều bằng a. Gọi M là trung điểm của CD. Tính cosin của góc giữa hai đường thẳng AD và BM.
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
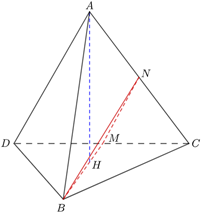
Kẻ MN // AD (M Î CD).
Góc giữa hai đường thẳng AD và BM là góc giữa hai đường thẳng MN và BM và là góc a.
Vì M là trung điểm của CD.
Nên BM là đường trung tuyến của tam giác đều BCD cạnh a.
Do đó .
Vì M là trung điểm của CD và MN // AD nên N cũng là trung điểm của AC.
Suy ra BN là đường trung tuyến của tam giác đều BCA cạnh a.
Do đó .
Vì M, N lần lượt là trung điểm của CD và AC nên MN là đường trung bình của tam giác ACD.
Suy ra
.
Do đó
Vậy cosin của góc giữa hai đường thẳng AD và BM là
Cho cấp số cộng (un). Biết un = -5n + 10 "n Î ℕ*. Tìm công sai d của cấp số công (un).
1. Cho cấp số cộng (un) có u3 = 6 và u10 = 34.
a) Tìm số hạng u1 và công sai d của cấp số cộng (un).
b) Tính tổng S = u1 + u2 + ... + u10.
2. Cho cấp số nhân (vn). Biết rằng ba số v1, v4 và v7 lần lượt là các số hạng thứ nhất, thứ hai và thứ mười của một cấp số cộng có công sai d ¹ 0. Hãy tìm công bội q của cấp số nhân (vn).
Cho cấp nhân (un) có số hạng u3 = -2 và u6 = 128. Tìm công bội q của cấp số nhân (un).
Cho cấp số nhân (un) có số hạng đầu u1 và công bội q ¹ 0. Công thức xác định số hạng tổng quát của cấp số nhân (un) là
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Gọi O là tâm của hình vuông ABCD. Biết SA ^ (ABCD) và SA = a.
a) Chứng minh rằng BC ^ (SAB) và CD ^ (SAD).
b) Chứng minh rằng BD ^ SC.
c) Gọi E là trung điểm của cạnh SC. Chứng minh rằng AE ^ SO và AE ^ (SBD).
d) Tính góc tạo bởi đường thẳng AC và mặt phẳng (SCD).
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a và BC = a. Biết SA ^ (ABCD) và SA = a. Góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng
Cho lăng trụ ABC.A’B’C’. Gọi M là trung điểm của B’C’. Đặt
Hãy biểu thị véc-tơ theo ba véc-tơ