Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành tâm O. Gọi M, N lần lượt là trung điểm SA, SD. Mặt phẳng (OMN) song song với mặt phẳng nào sau đây?
B. (SCD);
Giải bởi Vietjack
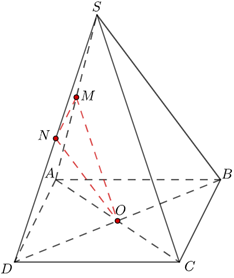
Vì M, N lần lượt là trung điểm của SA, SD nên suy ra MN là đường trung bình của ∆SAD.
Từ đó MN // AD // BC Þ MN // (SBC) (1)
Vì O, N lần lượt là trung điểm của BD, SD nên suy ra ON là đường trung bình của ∆SBD.
Từ đó ON // SB Þ ON // (SBC) (2)
Từ (1) và (2) nên suy ra (OMN) // (SBC).
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm thuộc cạnh BC và (a) là mặt phẳng đi qua điểm M và song song với mặt phẳng (SAB). Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (a) là một:
Cho cấp số cộng (un) có u7 = 27 và u20 = 79. Tổng 30 số hạng đầu của cấp số cộng này bằng
Cho một đường thẳng a song song với mặt phẳng (P). Có bao nhiêu mặt phẳng chứa a và song song với (P)?
Cho cấp số cộng (un) thoả mãn Số hạng đầu u1 và công sai d của cấp số cộng đã cho lần lượt là
Cho hình lăng trụ tam giác ABC.A’B’C’.
a) Gọi E, F lần lượt là tâm của các mặt bên ABB’A’ và ACC’A’. Chứng minh đường
thẳng EF song song mặt phẳng (BCC’B’).
b) Gọi G là trọng tâm của tam giác ABC và H là trung điểm của B’C’. Chứng minh đường thẳng C’G song song với mặt phẳng (A’BH).
Cho cấp số nhân (un) có u1 = 5 và công bội q = 2. Tổng của bốn số hạng đầu của cấp số nhân bằng
Cho cấp số nhân (un) có u4 = 6, u5 = 2. Tìm công bội q của cấp số nhân.
