Trong không gian Oxyz, hai mặt phẳng $4x-4y+2z-7=0$ và $2x-2y+z+4=0$chứa hai mặt của hình lập phương. Thể tích khối lập phương đó là:

Trong không gian với hệ trục Oxyz, mặt phẳng đi qua điểm A(1,3,−2) và song song với mặt phẳng $\left(P\right):2x-y+3z+4=0$là:

Viết phương trình mặt phẳng (P)  đi qua điểm M(1;0;−2) và vuông góc với hai mặt phẳng (Q),(R)  cho trước với $\left(Q\right):x+2y-3z+1=0$ và $\left(R\right):2x-3y+z+1=0$.

Phương trình mặt phẳng (P) đi qua điểm M(3;4;1) và giao tuyến của hai mặt phẳng $\left(Q\right):19x-6y-4z+27=0 và \left(R\right):42x-8y+3z+11=0$là:

Trong không gian với hệ tọa độ Oxyz, cho  A(1,−3,2),B(1,0,1),C(2,3,0). Viết phương trình mặt phẳng (ABC) .

Cho hai mặt phẳng (P) và (Q) lần lượt có phương trình $x+2y-2z+1=0$ và $x-2y+2z-1=0$. Gọi (S) là quỹ tích các điểm cách đều hai mặt phẳng (P) và (Q).  Tìm khẳng định đúng.

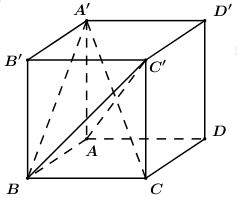
Cho hình lập phương ABCD.A′B′C′D′. Côsin góc giữa hai mặt phẳng $(A\text{'}BC)$và $(ABC\text{'})$bằng:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(4,−1,2),B(2,−3,−2) . Phương trình nào dưới đây là phương trình mặt phẳng trung trực của đoạn thẳng AB.

Trong không gian với hệ tọa độ  Oxyz, viết phương trình mặt phẳng qua điểm M(2,−3,4)  và nhận $\overrightarrow{n}=\left(-\mathrm{2,4,1}\right)$ làm vectơ pháp tuyến.

Cho mặt phẳng $\left(\alpha \right)$ đi qua hai điểm M(4;0;0) và N(0;0;3) sao cho mặt phẳng $\left(\alpha \right)$tạo với mặt phẳng (Oyz) một góc bằng 60⁰.  Tính khoảng cách từ điểm gốc tọa độ đến mặt phẳng $\left(\alpha \right)$

Trong không gian Oxyz, cho ba điểm A(1,0,0),B(0,1,0) và C(0,0,1). Phương trình mặt phẳng (P)  đi qua ba điểm A,B,C là:

Trong hệ trục toạ độ không gian Oxyz, cho A(1,0,0),B(0,b,0),C(0,0,c), biết b,c>0, phương trình mặt phẳng (P):y−z+1=0 . Tính $M=c+b$ biết$\left(ABC\right)\perp \left(P\right), d\left(O,\left(ABC\right)\right)=\frac{1}{3}$

Cho điểm A(1,2,−1) và điểm B(2,−1,3). Kí hiệu (S) là quỹ tích các điểm M(x,y,z) sao cho $M{A}^2-M{B}^2=2$. Tìm khẳng định đúng.

Cho hai điểm M(1;−2;−4),M′(5;−4;2). Biết M′ là hình chiếu của M lên mặt phẳng (P). Khi đó, phương trình (P) là:

Trong không gian với hệ toạ độ Oxyz, cho hai mặt phẳng $\left(P\right):x+2y+2z+11=0$và  $\left(Q\right):x+2y+2z+2=0$. Tính khoảng cách giữa (P) và (Q).

Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;1;2). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục $x\text{'}Ox,y\text{'}Oy,z\text{'}Oz$ lần lượt tại các điểm A,B,C sao cho $OA=OB=OC\ne 0$?