Trong không gian với hệ tọa độ Oxyz, cho mặt cầu và đường thẳng . Mặt phẳng vuông góc với Δ và cắt (S) theo giao tuyến là đường tròn (C) có bán kính lớn nhất. Phương trình là:
A.
B.
C.
 Giải bởi Vietjack
Giải bởi Vietjack
Đường thẳng có 1 VTCP là
Vì nên mặt phẳng có 1 VTPT là.Khi đó phương trình mặt phẳng có dạng
Mặt cầu có tâm I(4;−1;−1), bán kính
Gọi r là bán kính đường tròn
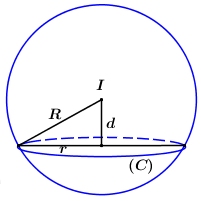
Áp dụng định lí Pytago ta có: do đó để r đạt GTLN thì d phải đạt GTNN (vì không đổi).
Ta có: suy ra
Vậy phương trình mặt phẳng cần tìm là:
Đáp án cần chọn là: D
Trong không gian Oxyz, cho mặt cầu và hai điểm A(2;1;0), B(0;2;0). Khi điểm S thay đổi trên mặt cầu (C), thể tích của khối chóp S.OAB có giá trị lớn nhất bằng bao nhiêu?
Trong không gian với hệ tọa độ Oxyz , phương trình nào dưới đây là phương trình mặt cầu tâm I(−3;2;−4) và tiếp xúc với mặt phẳng (Oxz)?
Cho điểm A(0;8;2) và mặt cầu (S) có phương trình và điểm B(1;1;−9). Viết phương trình mặt phẳng (P) qua A tiếp xúc với (S) sao cho khoảng cách từ B đến (P) là lớn nhất. Giả sử là véctơ pháp tuyến của (P). Lúc đó:
Mặt cầu (S) có tâm I(−1;2;−5) cắt mặt phẳng theo thiết diện là hình tròn có diện tích . Phương trình của (S) là:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu và mặt phẳng . Gọi M(a;b;c) là điểm trên mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) là lớn nhất. Khi đó:
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng và mặt phẳng song song với nhau. Biết A(1;2;1) là điểm nằm giữa hai mặt phẳng (P) và (Q). Gọi (S) là mặt cầu qua A và tiếp xúc với cả hai mặt phẳng (P) và (Q). Biết rằng khi (S) thay đổi thì tâm của nó luôn nằm trên một đường tròn. Tính bán kính r của đường tròn đó
Trong không gian vớ hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(3;2;−1) và đi qua điểm A(2;1;2). Mặt phẳng nào dưới đây tiếp xúc với (S) tại A?
Trong không gian với hệ tọa độ Oxyz cho mặt cầu và 2 đường thẳng . Một phương trình mặt phẳng (P) song song với và tiếp xúc với mặt cầu (S) là:
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(2;1;−1) và tiếp xúc với mặt phẳng có phương trình 2x−2y−z+3=0. Bán kính của (S) là:
Trong không gian Oxyz, cho đường thẳng và mặt phẳng . Gọi (S) là mặt cầu có tâm I thuộc ![]() và tiếp xúc với (P) tại điểm H(1;−1;0). Phương trình của (S) là:
và tiếp xúc với (P) tại điểm H(1;−1;0). Phương trình của (S) là:
Viết phương trình mặt cầu có tâm I(−1;2;3) và tiếp xúc với mặt phẳng
Trong không gian với hệ tọa độ Oxyz, cho mặt cầ. Gọi T là tập các giá trị của m để mặt cầu (S) tiếp xúc với mặt phẳng (Oyz). Tích các giá trị của m trong T bằng:
Trong không gian Oxyz, xác định tọa độ tâm I của đường tròn giao tuyến của mặt cầu với mặt phẳng.
Trong không gian với hệ tọa độ Oxyz,(α) cắt mặt cầu (S) tâm I(1;−3;3) theo giao tuyến là đường tròn tâm H(2;0;1) , bán kính r=2 . Phương trình (S) là: