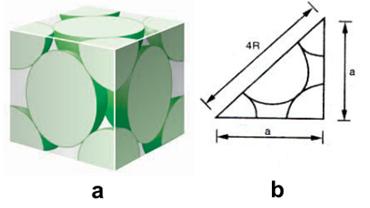
Ca (Canxi) có cấu trúc lập phương tâm diện, mỗi nguyên tử Ca có dạng hình cầu bán kính R. Một ô cơ sở của mạng tinh thể Ca là một hình lập phương có cạnh bằng a, mỗi mặt của hình lập phương chứa nguyên tử Ca và mỗi góc chứa nguyên tử Ca khác (Hình a, b)
A.68%
B.74%
C.72%
 Giải bởi Vietjack
Giải bởi Vietjack
Bước 1: Tính số nguyên tử Ca có trong một ô cơ sở
Số nguyên tử Ca trong một ô cơ sở gồm: 6 mặt mỗi mặt có khối cầu+8 góc khối cầu. Như thế số nguyên tử Ca là: nguyên tử.
Bước 2: Tính thể tích chiếm chỗ của Ca trong một ô cơ sở và thể tích của ô cơ sở.
Thể tích của 4 nguyên tử Ca là:
Thể tích của một khối lập phương là
Bước 3: Tính R theo a và độ đặc khít
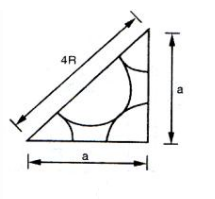
Theo hình vẽ ta thấy cạnh huyền: 4R, các cạnh góc vuông đều bằng a.
Theo định lý Pitago ta có:
Đáp án cần chọn là: B
Cho hình lăng trụ đứng có đáy là tam giác với độ dài cạnh đáy lần lượt 5cm,13cm,12cm. Một hình trụ có chiều cao bằng 8cm ngoại tiếp lăng trụ đã cho có thể tích bằng
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại và . Gọi (S) là mặt cầu ngoại tiếp hình chóp S.ABC. Tìm mệnh đề sai.
Cho một khối trụ có chiều cao bằng 8cm, bán kính đường tròn đáy bằng 6cm. Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục 4cm. Diện tích của thiết diện được tạo thành là :
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có độ dài cạnh đáy bằng a và chiều cao bằng h. Tính thể tích V của khối trụ ngoại tiếp lăng trụ đã cho.
Một hình nón có thiết diện qua trục là tam giác đều cạnh a. Tính bán kính mặt cầu ngoại tiếp hình nón theo a.
Cho hình hộp chữ nhật có . Tính bán kính R của mặt cầu ngoại tiếp tứ diện ABB′C′.
Một cái cột có hình dạng như hình bên (gồm một khối nón và một khối trụ ghép lại). Chiều cao đo được ghi trên hình, chu vi đáy là cm. Thể tích của cột bằng:
Cho khối trụ có hai đáy là hình tròn (O;R) và (O′;R), . Trên đường tròn tâm O lấy (O) lấy hai điểm A,B sao cho . Mặt phẳng (P) đi qua A,B cắt OO′ và tạo với đáy một góc bằng 600. (P) cắt khối trụ theo thiết diện là một phần của elip. Diện tích thiết diện đó bằng: