Cho , gọi D, E, F lần lượt là trung điểm của các cạnh AB, AC, BC; và M, N, P, Q theo thứ tự là trung điểm các đoạn thẳng DA, AE, EF, FD.
a) Chứng minh: EF là đường trung bình của tam giác ABC
b) Chứng minh: Các tứ giác DAEF; MNPQ là hình bình hành
c) Khi tam giác ABC vuông tại A thì các tứ giác DAEF; MNPQ là hình gì ? Chứng minh?
d) Tìm điều kiện của tam giác ABC để tứ giác MNPQ là hình vuông? Giải bởi Vietjack
Giải bởi Vietjack
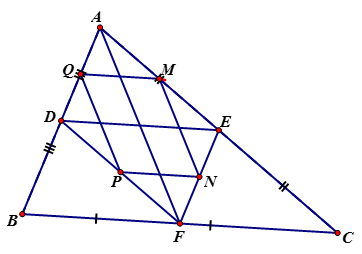
a) Ta có E là trung điểm AC, F là trung điểm BC nên EF là đường trung bình
b) Ta có EF là đường trung bình (cmt) mà D là trung điểm AB nên là hình bình hành
Xét có M, N lần lượt là trung điểm AD, AE
Cmtt là hình bình hànhc) Khi vuông tại A thì Hình bình hành DAEF có nên DAEF là hình chữ nhật.
Khi thì DAEF là hình chữ nhật
Mặt khác, theo tính chất đường trung bình ta có khi đó MN = NP
=> MNPQ là hình bình hành có MN = NP nên MNPQ là hình thoid) vuông tại A thì MNPQ là hình thoi. Để MNPQ là hình vuông thì mà
MN // DE, NP // AF (tính chất đường trung bình)
Nên mà DE // BC (tính chất đường trung bình)
Suy ra vuông tại A có AF là vừa đường trung tuyến, vừa đường cao
Nên vuông cân tại A
Vậy vuông cân tại A thì MNPQ là hình vuông.Cho vuông tại A M là trung điểm của là điểm nằm trong sao cho Trên tia đối của tia MP lấy điểm Q sao cho MP = MQ
a) Chứng minh: tứ giác APBQ là hình thoi.
b) Qua C vẽ đường thẳng song song với BP cắt tia QP tại E. Chứng minh tứ giác ACEQ là hình bình hành.
c) Gọi N là giao điểm của PE và BC. Chứng minh: AC = 2MN