Trong không gian Oxyz, cho hình bình hành ABCD có đỉnh A(-1; 4; 1), phương trình đường chéo , đỉnh C(a; b; c) thuộc mặt phẳng (P): x + 2y + z - 4 = 0. Khi đó giá trị của S = a + b + c là:
A. S = -2;
B. S = 2;
C. S = 6;
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
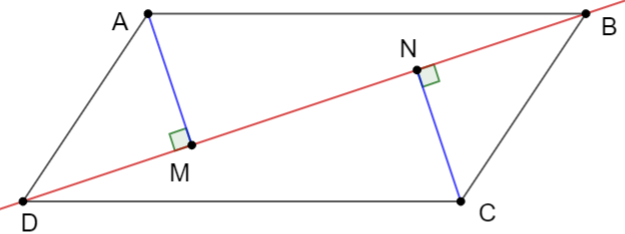
Ta có:
+)
+) Đỉnh C(a; b; c) thuộc mặt phẳng (P): x + 2y + z - 4 = 0
Þ a + 2b + c - 4 = 0 (1)
+)
Mặt phẳng (Q) vuông góc với BD nhận véc-tơ chỉ phương của đường thẳng BD làm véc-tơ pháp tuyến và đi qua A(-1; 4; 1) có phương trình
(Q): (x + 1) - (y - 4) - 2.(z - 1) = 0
Û x - y - 2z + 7 = 0
M là giao của mặt phẳng (Q) và đường thẳng BD nên ta có M(2 + m; 2 - m; -3 - 2m) Î (Q)
Þ (2 + m) - (2 - m) - 2.(-3 - 2m) + 7 = 0
Û 2 + m - 2 + m + 6 + 4m + 7 = 0
Û 6m + 13 = 0
Kẻ CN ^ BD. Dễ dàng chứng minh được
Mà điểm N Î BD nên suy ra
(2)
Thay (2) vào (1) ta được
(3)
Lại tiếp tục thay (3) vào (2) ta được
Khi đó giá trị của S = a + b + c là:
S = 3 + 2 - 3 = 2.
Cho các số thực x, y thỏa 3x + y - 3xi = 2y - 1 + (x - y)i. Khi đó giá trị của M = x + y là:
Trong không gian Oxyz, cho hai điểm A (1; 2; 3), B(1; 2; 1) và M là một điểm nằm trên mặt phẳng Oxy. Tìm tọa độ điểm M để đạt giá trị nhỏ nhất.
Trên mặt phẳng Oxy, gọi A, B, C lần lượt là các điểm biểu diễn các số phức Khi đó tam giác ABC là:
Trong không gian Oxyz, cho hai điểm A(2; 1; 0), B(-2; 3; 2) và đường thẳng Phương trình mặt cầu đi qua hai điểm A, B và có tâm nằm trên đường thẳng d là:
Trong không gian Oxyz, cho bốn điểm A(2; -1; 6), B(-3; -1; -4), C(5; -1; 0), D(1; 2; 1). Thể tích của tứ diện ABCD là:
Gọi S là diện tích của hình phẳng giới hạn bởi các đồ thị hàm số y = x2 + 3 và y = 4x. Mệnh đề nào sau đây đúng?