Trong các số phức z thỏa mãn điều kiện |z - 3 + 4i| = 2. Tính mô đun lớn nhất của số phức z.
A. |z| = 7;
B.
C.
D. |z| = 3.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
Gọi z = x + yi
Ta có: |z - 3 + 4i| = 2
Û (x - 3)2 + (y + 4)2 = 4
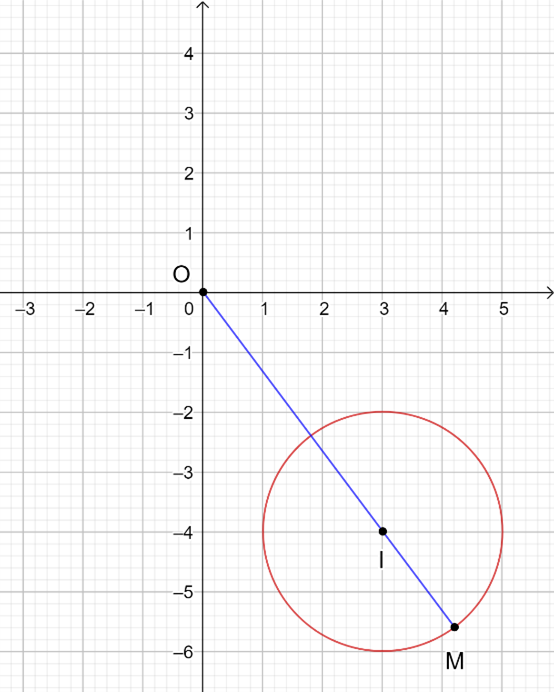
Vậy M(x; y) là điểm của số phức z trên hệ trục tọa độ và M thuộc đường tròn tâm I(3; -4) bàn kính R = 2
Mô đun của số phức z là .
Vậy mô đun của số phức z lớn nhất khi OM lớn nhất.
OM lớn nhất khi và chỉ khi M nằm trên đường thẳng OI và xa O nhất
Þ OM = OI + IM
Vậy mô đun của số phức z lớn nhất bằng 7.
Trong không gian Oxyz, tìm tọa độ điểm H là hình chiếu vuông góc của điểm M(2; 3; -1) trên mặt phẳng (P): x - y + 2z - 3 = 0.
Tính thể tích khối tròn xoay tạo nên khi ta cho hình phẳng giới hạn bởi các đường quay quanh trục Ox
Tính thể tích khối tròn xoay tạo nên khi cho hình phẳng giới hạn bởi , Ox, x = 0, x = 2 quay quanh trục Ox.
Trong không gian Oxyz, cho A(1; 2; -1), B(3; 1; 0). Tính độ dài đoạn thẳng AB.
Cho hàm số y = f (x) liên tục trên [a; b]. Thể tích khối tròn xoay được sinh ra khi cho hình phẳng giới hạn bởi đồ thị y = f (x), Ox, x = a, x = b quay xung quanh Ox là
Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua A(1; 0; 0), B(0; -1; 0), C(0; 0; 2)
Gọi z0 là nghiệm phức có phần ảo dương của phương trình z2 + 2z + 10 = 0. Điểm nào sau đây là điểm biểu diễn số phức z0?
Trong không gian Oxyz, cho mặt phẳng (P): 2x + y - 3z - 5 = 0. Phương trình chính tắc của đường thẳng (d) đi qua A(3; -2; 4) và vuông góc mp (P) là