Cho hình chóp tứ giác đều có độ dài cạnh bên là 5cm, chiều cao của hình chóp là 4cm. Tính:
a) Diện tích xung quanh của hình chóp
b) Thể tích của hình chóp.
Giải bởi Vietjack
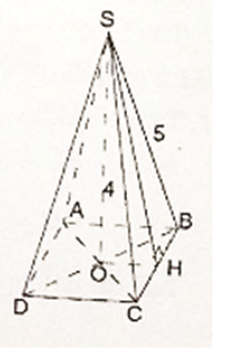
a) Ta có
OC2 = SC2 - SO2 (Pytago)
= 52 - 42 = 9(cm)
=> OC = 3(cm)
=> AC = 6(cm)
AB2 + BC2 = AC2 (pytago)
2BC2 = AC2 (do AB = BC)
BC2 = AC2/2 = 36/2 = 18(cm)
BC = √18 = 3√2 (cm)
Gọi K là trung điểm của BC. Tam giác SBC cân tại S có SH là đường trung tuyến nên SH cũng là đường cao. Suy ra SH ⊥ BC
Do đó
Cho hình hộp chữ nhật MNPQ.EFGH
a) Tìm giao tuyến của hai mặt phẳng (MNFE) và (QNFH).
b) Chứng minh: QH ⊥ mp(EFGH)
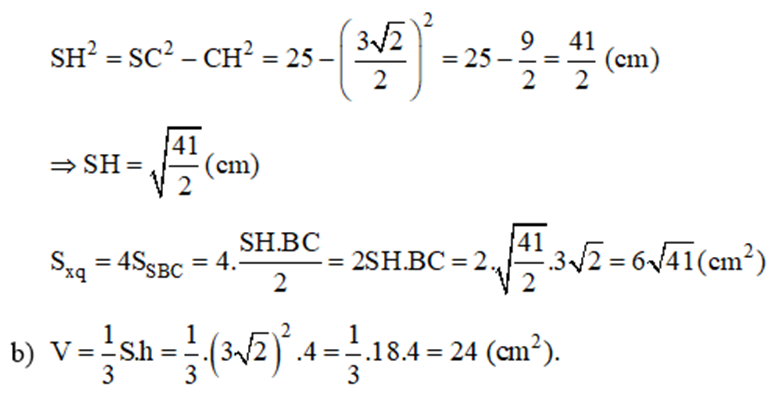
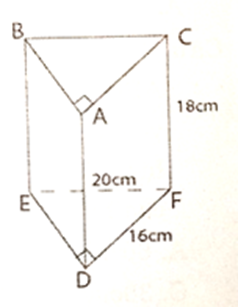
Cho một hình lăng trụ đứng ABC.DEF, đáy là tam giác vuông có kíc thước như hình bên. Thể tích hình lăng trụ này là:
Chọn câu có khẳng định sai.
Hình chóp tam giác đều có chân đường cao trùng với:
