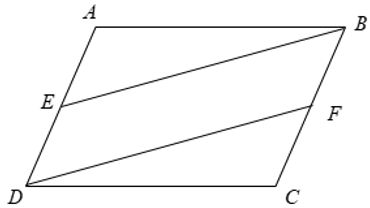
Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh BE = DF và .
Giải bởi Vietjack
Xét tứ giác BEDF có
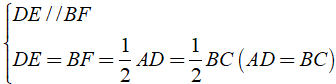
⇒ BEDF là hình bình hành
⇒ BE = DF (hai cạnh đối song song và bằng nhau)
Ta có: ABCD là hình bình hành nên ( 1 )
BEDF là hình bình hành nên ( 2 )
Mà
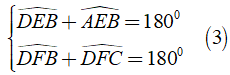
Từ ( 2 ) và ( 3 ) ⇒ ( 4 )
Xét Δ ABE có = 1800 (5)
Xét Δ DFC có = 1800 (5)
Từ ( 1 ), ( 4 ), ( 5 ) ⇒ (đpcm)
Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của AB, CD. Đường chéo BD cắt AK, AI lần lượt tại M, N. Chứng minh rằng:
a) AK//CI
Cho hình bình hành ABCD có H, K lần lượt là các chân đường cao kẻ từ đỉnh A,C xuống BD.
a) Chứng minh AHCK là hình bình hành.
