Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Chứng minh tứ giác AHCE là hình chữ nhật.
Giải bởi Vietjack
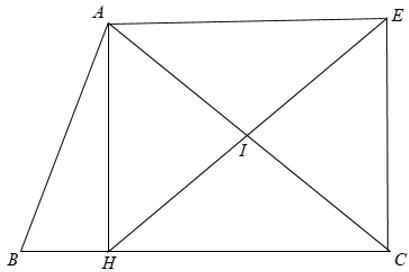
+ Trong Δ AHC vuông có I là trung điểm của AC
⇒ HE là đường trung tuyến của Δ AHC.
⇒ HI = AC = AI = IC.
Mà E đối xứng với H qua I ⇒ HI = IE.
Khi đó ta có HI = IE = AI = IC.
+ Xét Δ HCE có CI là đường trung tuyến ứng với cạnh HE
mà CI = HE ⇒ Δ HCE vuông tại C.
Tương tự xét với Δ AHE,Δ AEC đều là các tam giác vuông tại A, E.
Xét tứ giác AHCE có = 900
⇒ AHCE là hình chữ nhật.Tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì ? Giải thích ?
