Cho hai điểm A, B cùng nằm trên một nửa mặt phẳng có bờ là đường thẳng d. Tìm trên d điểm M sao cho tổng MA + MB nhỏ nhất.
Giải bởi Vietjack
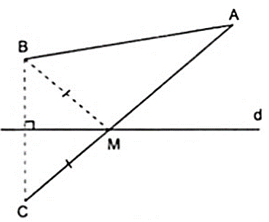
Vẽ điểm C đối xứng với B qua đường thẳng d, giả sử tìm được điểm M trên d thì MB = MC ( 1 ).
Do A, B, d cố định nên C cũng cố định suy ra độ dài đoạn AC không đổi.
Áp dụng bất đẳng thức tam giác ta có vào Δ AMC ta được: MA + MC ≥ AC ( 2 )
Dấu bằng xảy ra khi M nằm giữa A và C hay M là giao điểm của AC và đường thẳng d
Từ ( 1 ) và ( 2 ) suy ra MA + MB nhỏ nhất bằng AC khi M là giao điểm của AC và đường thẳng d
Cho hình vuông ABCD. Gọi I,K lần lượt là trung điểm của AD và DC.
a) Chứng minh rằng BI ⊥ AK.
