Cho hình thoi ABCD. Gọi O là giao điểm hai đường chéo AC và BD. Đường thẳng qua O không song song với AD cắt AB tại M và CD tại N.
a) Chứng minh ΔAOM = ΔCON.
Giải bởi Vietjack
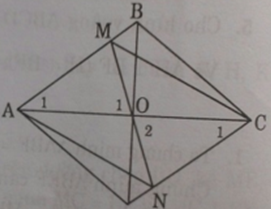
a) Xét ΔAOM và ΔCON có:
∠A1 = ∠C1 (so le trong)
AO = CO (tính chất đường chéo hình thoi)
∠O1 = ∠O1 (đối đỉnh)
Vậy ΔAOM = ΔCON. (c.g.c) ⇒ OM = ON
Cho tứ giác ABCD có BD là phân giác ∠B và BC = CD. Chứng minh tứ giác ABCD là hình thang.
Cho tứ giác ABCD. Gọi P, Q, R, S lần lượt là trung điểm của AB, AC, CD, DB.
1. Chứng minh tứ giác PQRS là hình bình hành.
Hãy điền vào chỗ (…) để được các khẳng định đúng:
Hình thang là tứ giác có ………
