 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Nhập vào máy tính biểu thức sau:
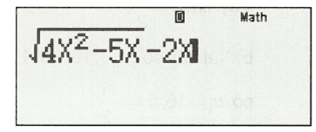
Sau đó bấm CACL.
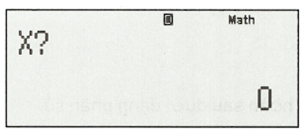
Nhập: sau đó bấm “=”, ta được kết quả:
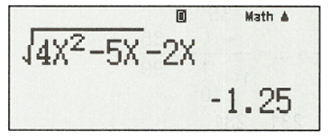
Kết quả: Vậy giới hạn của dãy số bằng
Trong các khẳng định sau
(I) f(x) liên tục trên đoạn và thì phương trình f(x)=0 có nghiệm
(II) f(x) không liên tục trên và thì phương trìnhf(x)=0 vô nghiệm
(III) f(x) liên tục trên đoạn và thì tồn tại ít nhất một số sao cho
(IV) f(x) liên tục trên đoạn và thì tồn tại ít nhất một số sao cho
Số khẳng định đúng là
Cho các số thực a, b, c thỏa mãn và . Khi đó số nghiệm thực phân biệt của phương trình bằng
Cho phương trình . Khẳng định nào sau đây đúng?
A. Phương trình đã cho không có nghiệm trong khoảng
B. Phương trình đã cho chỉ có một nghiệm trong khoảng
C. Phương trình đã cho có ít nhất một nghiệm trong khoảng
D. Phương trình đã cho không có nghiệm trong khoảng
Cho phương trình (1) trong đó a, b, c là các tham số thực. Chọn khẳng định đúng trong các khẳng định sau
A. Phương trình (1) vô nghiệm với mọi a, b, c
B. Phương trình (1) có ít nhất một nghiệm với mọi a, b, c
C. Phương trình (1) có ít nhất hai nghiệm với mọi a, b, c
D. Phương trình (1) có đúng ba nghiệm phân biệt với mọi a, b, c