 Giải bởi Vietjack
Giải bởi Vietjack
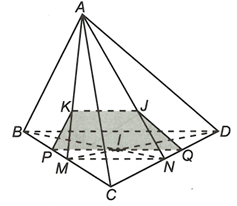
Gọi M và N lần lượt là trung điểm của BC và CD.
Do K, J lần lượt là trọng tâm của tam giác ABC và ACD nên
Áp dụng định lý Ta-lét suy ra KJ // MN
Suy ra trong đó
Giả sử Ix cắt BC, CD lần lượt tại P và Q. Vậy thiết diện của mặt phẳng (KIJ) với tứ diện ABCD là tứ giác KPQJ.
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi H và K lần lượt là trung điểm các cạnh CB và CD, M là điểm bất kì trên cạnh SA. Dựng thiết diện của hình chóp với mặt phẳng (MHK)
Cho tứ diện ABCD có AB vuông góc với CD, tam giác BCD vuông tại C và góc M là một điểm thay đổi trên cạnh BD; đặt Mặt phẳng đi qua M và song song với AB, CD.
a) Dựng thiết diện của tứ diện với