Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB là đáy lớn). Gọi I, J lần lượt là trung điểm của SA, SB; M là điểm tùy ý trên SD (M khác S và D).
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
 Giải bởi Vietjack
Giải bởi Vietjack
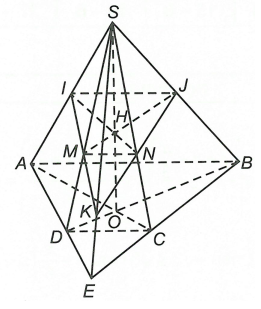
a) Gọi .
Ta có E là điểm chung của và (SBC)
Lại có , S là điểm chung của (SAD) và (SBC).
VậyCho tứ diện đều ABCD có cạnh bằng a. Mặt phẳng (P) thay đổi song song với AD và BC cắt AB, AC, CD, BD lần lượt tại M, N, P, Q. Giả sử AM=x, . Diện tích thiết diện MNPQ đạt giá trị lớn nhất khi
Cho hai đường thẳng a, b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b?
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là hai điểm trên SA, SB sao cho . Vị trí tương đối giữa MN và (ABCD) là
Cho hình chóp S.ABCD có ABCD là hình bình hành. Gọi I, J, E, F lần lượt là trung điểm SA, SB, SC, SD. Trong các đường thẳng sau, đường thẳng nào không song song với IJ?
d) Gọi H là giao điểm của IN và JM. Khi M di chuyển trên SD hãy chứng minh rằng H di chuyển trên một đường thẳng cố định.