Cho hình chóp S.ABCD. Gọi O là giao điểm của AC và BD. Xét hai mệnh đề
(I). Nếu ABCD là hình bình hành thì .
(II). Nếu thì ABCD là hình bình hành.
Mệnh đề nào đúng?
A. Chỉ (I).
B. Chỉ (II).
C. Không có.
D. Cả (I) và (II).
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn đáp án D
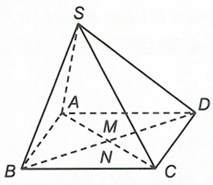
Gọi M, N lần lượt là trung điểm của AC và BD. Do O là giao điểm của AC và BD nên
là hình bình hành.
Vậy mệnh đề (I) và (II) đều đúng.
Bình luận: Để chứng minh mệnh đề (I) và (II) đúng, ta áp dụng: Cho và .
Khi đó .
Chứng minh: Nếu A không trùng O thì B không trùng O (do ) và
Nhưng thẳng hàng (trái với giả thiết )
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng
Cho hình hộp ABCD.A'B'C'D'. Sử dụng các đỉnh của hình hộp làm điểm đầu và điểm cuối của vectơ.
a) Hãy kể tên các vectơ bằng nhau lần lượt bằng các vectơ
Trong không gian cho ba vectơ . Cho các khẳng định sau.
(1) Nếu các vectơ đồng phẳng thì các vectơ thuộc một mặt phẳng nào đó.
(2) Nếu các vectơ đồng phẳng thì ba vectơ cùng phương.
(3) Nếu tồn tại hai số thực m, n sao cho thì các vectơ đồng phẳng.
(4) Nếu các vectơ đồng phẳng thì giá của chúng song song với mặt phẳng nào đó.
Có bao nhiêu khẳng định đúng?
Cho hình hộp ABCD.A'B'C'D'. Gọi G, G' lần lượt là trọng tâm của các tam giác . Chứng minh các điểm thẳng hàng.