Cho hình thang ABCD , AD cắt BC tại I, AC cắt BD tại O. M, N lần lượt là trung điểm của AB, DC. Chứng minh rằng I, M, O, N thẳng hàng.
 Giải bởi Vietjack
Giải bởi Vietjack
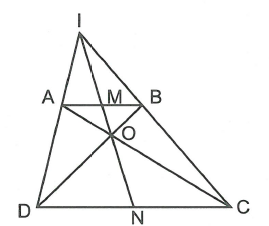
Vì M là trung điểm AB, N là trung điểm CD nên
Mà nên AC, MN, BD đồng quy hay O thuộc MN (1 ).
Lại có:
mà nên AD, MN, BC đồng quy hay I thuộc MN (2).
Từ (1 ) và (2) suy ra I, M, O, N thẳng hàng.
Nhận xét:
- Đây là bài toán đơn giản tuy nhiên được sử dụng rất nhiều với tên gọi Bổ đề hình thang: "Trong hình thang có hai cạnh đáy không bằng nhau, đường thẳng đi qua giao điểm của các đường thẳng chứa hai cạnh bên thì đi qua trung điểm của hai đáy"
- Ngược lại: Trong hình thang có hai cạnh đáy không bằng nhau, giao điểm của hai cạnh bên, giao điểm của hai đường chéo và trung điểm của hai đáy là các điểm thẳng hàng".
Cho tam giác ABC, O là một điểm thuộc miền trong tam giác. Qua O kẻ HF song song với BC, DE song song với AB, MK song song với AC (H, K thuộc AB; E, M thuộc BC; D, F thuộc AC). Chứng minh rằng:
Cho tứ giác lồi ABCD. Gọi O là giao điểm của AC và BD. Gọi I, K, H lần lượt là chân đường cao kẻ từ B, O, C tới AD. Chứng minh rằng .
Cho tam giác ABC với đường phân giác AD thỏa mãn . Tính số đo góc BAC.
Cho hình vuông ABCD. Trên cạnh AB lấy điểm I. Gọi E là giao điểm của DI và CB. Gọi J là giao điểm của AE và CI. Chứng minh BJ vuông góc với DE.
Cho tam giác ABC nhọn AH là đường cao. Trên AH, AB, AC lần lượt lấy điểm D, E, F sao cho . Chứng minh rằng EF//BC.