Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy hai điểm D, E sao cho BD = DE = EC. Qua D và E kẻ các đường vuông góc với BC, chúng cắt AB, AC lần lượt ở K và H. Tứ giác KHED là hình gì? Vì sao?
 Giải bởi Vietjack
Giải bởi Vietjack
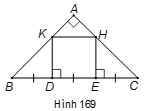
Tứ giác KHED là hình vuông.
Giải thích: Tam giác vuông BDK có nên là tam giác cân,
do đó BD = DK. Chứng minh tương tự, HE = EC.
Vì BD = DE = EC theo giả thiết, nên:
KD = DE = EH.
Tứ giác KHED có nên là hình bình hành.
Hình bình hành này lại có nên nó là hình chữ nhật.
Hình chữ nhật này lại có KD = DE nên nó là hình vuông.
Các câu sau đúng hay sai?
a) Hình chữ nhật có hai đường chéo bằng nhau là hình vuông.
b) Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
c) Hình thoi có hai đường chéo vuông góc với nhau là hình vuông.
d) Hình thoi có hai đường chéo bằng nhau là hình vuông.
Nêu các tính chất về đường chéo của hình vuông. Chỉ rõ tính chất nào có ở hình bình hành, ở hình chữ nhật, ở hình thoi.
Tứ giác có bốn cạnh bằng nhau và hai đường chéo vuông góc có phải là hình vuông không? Nếu không hãy sửa lại một dấu hiệu để tứ giác là hình vuông.