Cho hình vẽ. So sánh đúng là
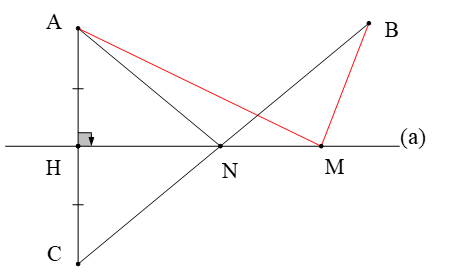
A. BC > MA + MB;
B. BC = MA + MB;
C. BC < MA + MB;
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
Ta có a ⊥ AC tại H và HA = HC
Do đó a là đường trung trực của AC
N ∈ a ⇒ NA = NC (tính chất đường trung trực)
Suy ra NA + NB + NC + NB = BC
Hay BC = NA + NB
M ∈ a ⇒ MA = MC (tính chất đường trung trực)
Do đó: MA + MB = MC + MB
Xét ∆BCM có:
MC + MB > BC (bất đẳng thức trong tam giác)
Do đó BC < MA + MB.
Cho tam giác có một đường phân giác đồng thời là đường trung trực ứng với cùng một cạnh thì tam giác đó là tam giác
Trong ∆ABC hai đường trung trực của hai cạnh AB và AC cắt nhau tại D nằm trên cạnh C. Khẳng định đúng nhất là
Cho ∆ABC cân tại A, trung tuyến AM, đường trung trực của AC cắt AM ở D. Khẳng định đúng là
Cho tam giác ABC cân tại A có góc A bằng 40°. Đường trung trực của AB cắt AB tại H, cắt BC tại D. Số đo góc ADB là
Cho ∆MAB, ∆NAB, ∆PAB là ba tam giác cân chung đáy AB. Khẳng định đúng là
Đường trung trực của đoạn AB cắt AB tại H. Hai điểm M, N là hai điểm trên đường trung trực đó (N nằm giữa M và H). Gọi N’ là giao điểm của AN và BM. Khẳng định sai là
