Cho ∆MAB, ∆NAB, ∆PAB là ba tam giác cân chung đáy AB. Khẳng định đúng là
A. M, N, P trùng nhau;
B. M, N, P thẳng hàng;
C. M, N, P không thẳng hàng;
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
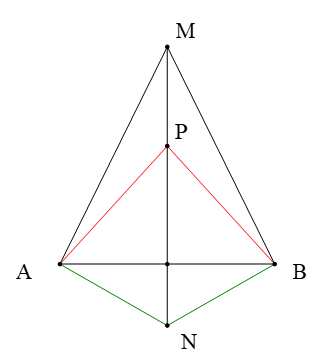
∆MAB cân tại M nên MA = MB. Do đó M thuộc đường trung trực của AB.
∆NAB cân tại N nên NA = NB. Do đó N thuộc đường trung trực của AB.
∆PAB cân tại P nên PA = PB. Do đó P thuộc đường trung trực của AB.
Suy ra M, N, P cùng thuộc đường trung trực của AB.
Do đó M, N, P thẳng hàng.
Cho tam giác có một đường phân giác đồng thời là đường trung trực ứng với cùng một cạnh thì tam giác đó là tam giác
Trong ∆ABC hai đường trung trực của hai cạnh AB và AC cắt nhau tại D nằm trên cạnh C. Khẳng định đúng nhất là
Cho ∆ABC cân tại A, trung tuyến AM, đường trung trực của AC cắt AM ở D. Khẳng định đúng là
Cho tam giác ABC cân tại A có góc A bằng 40°. Đường trung trực của AB cắt AB tại H, cắt BC tại D. Số đo góc ADB là
Đường trung trực của đoạn AB cắt AB tại H. Hai điểm M, N là hai điểm trên đường trung trực đó (N nằm giữa M và H). Gọi N’ là giao điểm của AN và BM. Khẳng định sai là
