Cho tứ diện OABC có OA, OB, OC đôi một vuông góc. Kẻ
a) Khẳng định nào đúng nhất?
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A
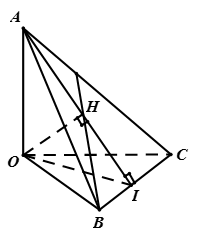
a) Ta có 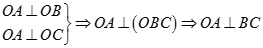
Lại có 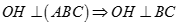
Vậy 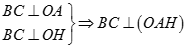
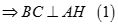
Tương tự
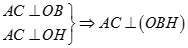
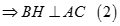
Từ (1) và (2) suy ra H là trực tâm của tam giác ABC
Trong mặt phẳng cho đường tròn đường kính cố định BC và M là điểm di động trên đường tròn này. Trên đường thẳng d vuông góc với tại B lấy một điểm A.
a) Khẳng định nào sau đây là đúng?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, 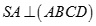 và
và
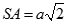 . Giả sử tồn tại tiết diện của hình chóp với mặt phẳng đi qua A vuông góc với SC. Tính diện tích thiết diện.
. Giả sử tồn tại tiết diện của hình chóp với mặt phẳng đi qua A vuông góc với SC. Tính diện tích thiết diện.Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, BC = , mặt bên SBC là tam giác vuông tại B, mặt bên SCD vuông tại D và SD = a
a) Tính SA.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh Gọi (P) là mặt phẳng đi qua A và vuông góc với BC. Thiết diện của hình chóp S.ABC được cắt bởi (P) có diện tích bằng?
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, và SA = a . Gọi I, K lần lượt là trung điểm các cạnh AB và SC. Tính IK.