 Giải bởi Vietjack
Giải bởi Vietjack
Chọn B
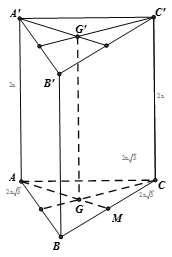
Gọi M là trung điểm BC. Khi đó ta dễ dàng tính được : 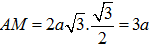
Vì G là trọng tâm tam giác ABC nên:
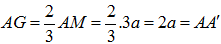
Cho hình chóp tứ giác S.ABCD, có đáy ABCD là hình thoi tâm I cạnh bằng a và góc , cạnh SC = và SC vuông góc với mặt phẳng (ABCD). Trong tam giác SCA kẻ tại K. Tính độ dài IK được
Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Người ta lấy trên giao tuyến d của hai mặt phẳng đó hai điểm A và B sao cho AB = 8. Gọi C là một điểm trên (P) , D là một điểm trên (Q) sao cho AC, BD cùng vuông góc với giao tuyến d và AC = 6, BD = 24. Độ dài CD là: