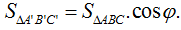Dạng 3: Tính độ dài đoạn thẳng, diện tích hình chiếu, chu vi và diện tích đa giác có đáp án
-
945 lượt thi
-
16 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Chọn A
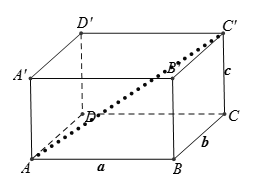
Từ sách giáo khoa, đường chéo hình hộp chữ nhật
Câu 2:
 Xem đáp án
Xem đáp án
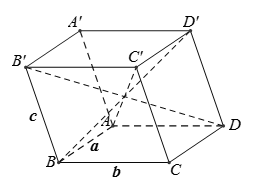
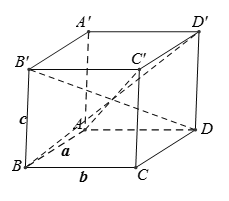
AC' = BD' => hình bình hành ABC'D' là hình chữ nhật
BD' = B'D => hình bình hành BDD'B' là hình chữ nhật
AC' = B'D => hình bình hành ADC'B' là hình chữ nhật
Câu 3:
Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Người ta lấy trên giao tuyến d của hai mặt phẳng đó hai điểm A và B sao cho AB = 8. Gọi C là một điểm trên (P) , D là một điểm trên (Q) sao cho AC, BD cùng vuông góc với giao tuyến d và AC = 6, BD = 24. Độ dài CD là:
 Xem đáp án
Xem đáp án
Chọn D
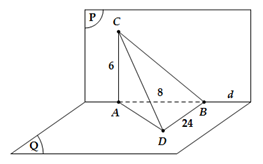
Ta có
Tam giác BCD vuông tại B nên
Câu 4:
 Xem đáp án
Xem đáp án
Chọn C.
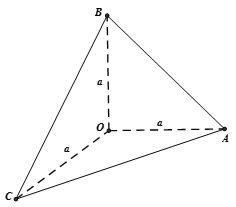
+ Áp dụng định lý Pytago trong tam giác OAB vuông tại O ta có:
Hoàn toàn tương tự ta tính được
là tam giác đều. Mặt khác theo giả thiết OA = OB = OC = a => các mặt bên của hình chóp O.ABC là các tam giác cân tại O => O.ABC là hình chóp đều => đáp án A đúng.
+ Chu vi là: đáp án C sai.
+ Nửa chu vi Diện tích là: . Diện tích là:
(đvdt).
=> đáp án B đúng.
+ Dễ chứng minh được
=> đáp án D đúng.
Câu 5:
 Xem đáp án
Xem đáp án
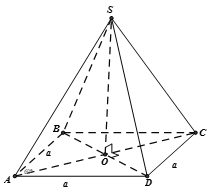
Xét có là tam giác đều cạnh a.
Vì O là tâm của ABCD nên suy ra AO là đường trung tuyến trong đều cạnh a nên dễ tính được .
Mặt khác theo giả thiết SAC là tam giác đều
Câu 6:
 Xem đáp án
Xem đáp án
Chọn B.
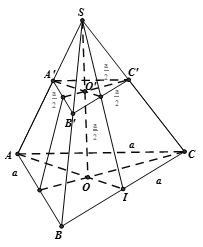
+ Đáp án A đúng.
+ Gọi I là trung điểm của BC
Từ giả thiết dễ dàng chỉ ra được 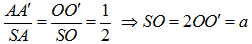 .
.
Mặt khác tam giác ABC là tam giác đều cạnh a, có AI là đường trung tuyến
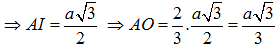
Áp dụng định lý Pytago trong tam giác SOA vuông tại O ta có:
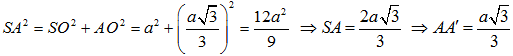
+ Ta có: 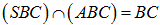 . Vì tam giác SBC cân tại S và I là trung điểm của BC nên suy ra
. Vì tam giác SBC cân tại S và I là trung điểm của BC nên suy ra 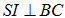 . Mặt khác
. Mặt khác 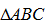 là tam giác đều có I là trung điểm của BC =>
là tam giác đều có I là trung điểm của BC => 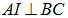
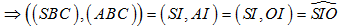
=> đáp án C đúng.
+ Ta có: 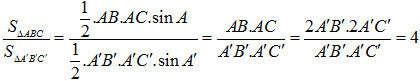
=> đáp án D đúng.
Câu 7:
 Xem đáp án
Xem đáp án
Chọn A
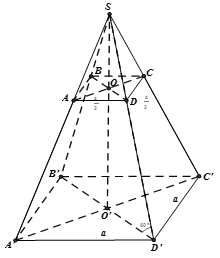
Ta có 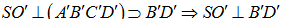 => O'D' là hình chiếu vuông góc của SD' lên (A'B'C'D')
=> O'D' là hình chiếu vuông góc của SD' lên (A'B'C'D')
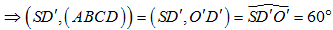
Từ giả thiết dễ dàng chỉ ra được 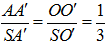
Vì tam giác A'D'C' là tam giác vuông cân tại D' có D'O' là đường cao nên ta có:
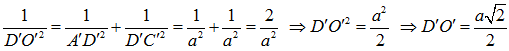
Áp dụng hệ thức lượng trong tam giác SD'O' vuông tại O' ta có:
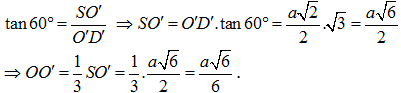
Câu 8:
 Xem đáp án
Xem đáp án
Chọn B.
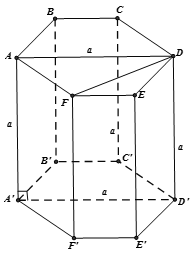
Tổng số đo các góc của hình lục giác là 4.180o = 720o. Vì ABCDEF là hình lục giác đều nên mỗi góc của hình lục giác đều ABCDEF là 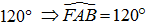 . Vì ABCDEF là hình lục giác đều nên ta suy ra:
. Vì ABCDEF là hình lục giác đều nên ta suy ra:
+ AD là tia phân giác của góc 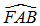 và
và 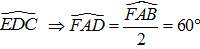
+ Tam giác AFD vuông tại F.
Xét tam giác AFD vuông tại F có 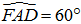 và ta suy ra:
và ta suy ra:
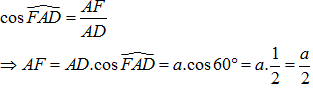
Câu 9:
 Xem đáp án
Xem đáp án
Chọn A
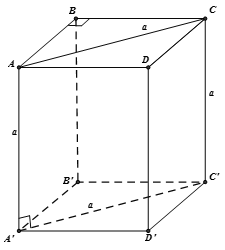
Từ giả thiết ta suy ra tam giác ABC vuông cân tại B => 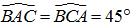
Áp dụng hệ thức lượng trong tam giác ABC vuông cân tại B có 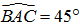 và cạnh AC = a, ta có:
và cạnh AC = a, ta có:
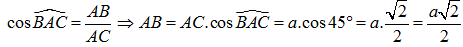
Câu 10:
 Xem đáp án
Xem đáp án
Chọn B
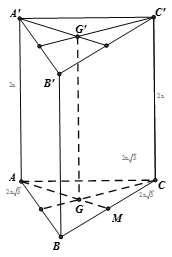
Gọi M là trung điểm BC. Khi đó ta dễ dàng tính được : 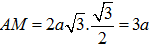
Vì G là trọng tâm tam giác ABC nên:
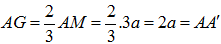
Câu 11:
 Xem đáp án
Xem đáp án
Chọn C
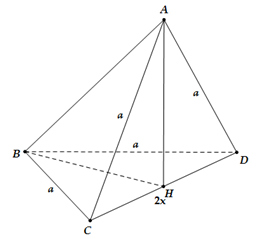
Gọi H là trung điểm của CD. Vì tam giác ACD cân tại A và tam giác BCD cân tại B nên 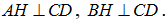
Ta có .
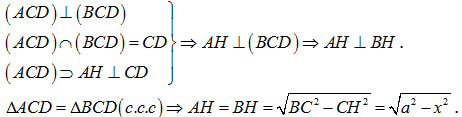
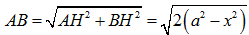
Câu 12:
 Xem đáp án
Xem đáp án
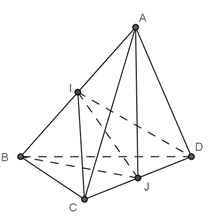
Ta có:
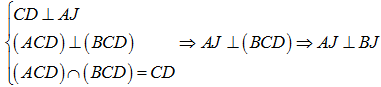
Vậy tam giác ABJ vuông tại J
Ta có:
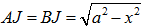
Do đó tam giác ABJ vuông cân tại J.
Suy ra 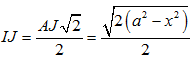
Câu 13:
 Xem đáp án
Xem đáp án
Chọn A.
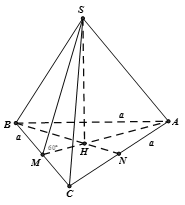
Ta có: 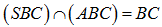
Gọi M, N lần lượt là trung điểm của các cạnh BC và AC
Dễ chứng minh được 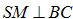 và
và 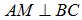
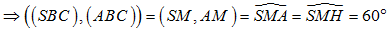
Ta dễ tính được: 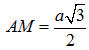
Vì H là chân đường cao của hình chóp đều S.ABC nên H trùng với trọng tâm của tam giác ABC
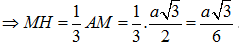
Áp dụng hệ thức lượng trong tam giác SHM vuông tại H ta có :
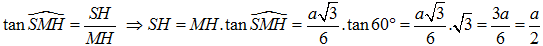
Câu 14:
 Xem đáp án
Xem đáp án
Chọn D.
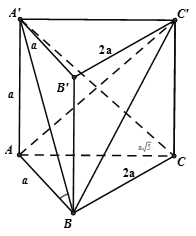
+ Cách 1: Chứng minh trực tiếp chỉ ra D là đáp án sai.
Từ giả thiết dễ dàng suy ra CC' = AA' = a.
Áp dụng định lý Pytago trong tam giác ACC' vuông tại C ta có:
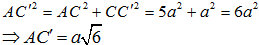
=> đáp án D sai.
+ Cách 2: Chứng minh 3 đáp án A, B, C đều đúng
=> ra đáp án D sai.
Câu 15:
Cho hình chóp tứ giác S.ABCD, có đáy ABCD là hình thoi tâm I cạnh bằng a và góc , cạnh SC = và SC vuông góc với mặt phẳng (ABCD). Trong tam giác SCA kẻ tại K. Tính độ dài IK được
 Xem đáp án
Xem đáp án
Chọn A
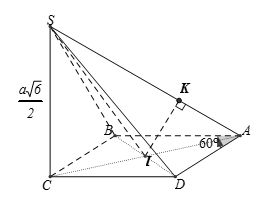
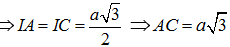
Tam giác AKI đồng dạng tam giác ACS
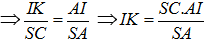
Tam giác BCD và tam giác ABD đều cạnh a
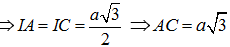
Tam giác SAC vuông tại C
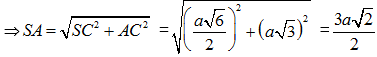
Vậy 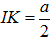
Câu 16:
 Xem đáp án
Xem đáp án
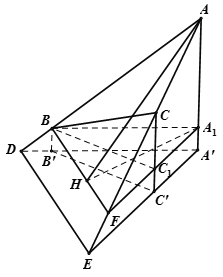
Qua B kẻ mặt phẳng (Q) // (P) cắt AA', CC' lần lượt tại A1 ; C1 khi đó 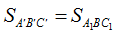
Góc giữa mặt phẳng (P) và mặt phẳng (ABC) bằng góc giữa mặt phẳng (ABC) và (BA1C1) và bằng
Kẻ 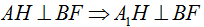
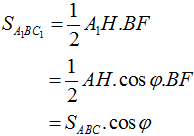
Vậy