Trắc nghiệm Toán 11 Bài 2: Phương trình lượng giác có đáp án (Mới nhất)
-
1559 lượt thi
-
141 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 3:
Phương trình có số nghiệm thuộc đoạn là
 Xem đáp án
Xem đáp án
Ta có , ( ).
Theo đề .
Mà .
Vậy có nghiệm thỏa yêu cầu bài toánCâu 4:
 Xem đáp án
Xem đáp án
Ta có:
,.
Nghiệm trên đoạn ứng với .
Vì nên chọn , k=1 .
Vậy trên đoạn phương trình đã cho có 2 nghiệm.
Chọn C
Câu 5:
Nghiệm của phương trình lượng giác: thỏa điều kiện là
 Xem đáp án
Xem đáp án
Vì nên chỉ có nghiệm .
Chọn A
Câu 8:
Tổng các nghiệm thuộc khoảng của phương trình là
 Xem đáp án
Xem đáp án
Vì x thuộc khoảng nên có 2 nghiệm thỏa mãn là ;
Vậy tổng các nghiệm bằng .
Chọn B
Câu 11:
Tìm số nghiệm của phương trình ?
 Xem đáp án
Xem đáp án
Ta có:
A.
+ Ta có:
B.
C.
D.
Vậy phương trình có 3 nghiệm .
Chọn B
Câu 12:
Điều kiện để phương trình: vô nghiệm là
 Xem đáp án
Xem đáp án
Phương trình vô nghiệm khi và chỉ khi
Chọn D
Câu 13:
Tập hợp tất cả các giá trị của m để phương trình có nghiệm là
 Xem đáp án
Xem đáp án
Phương trình có nghiệm khi .
Chọn D
Câu 14:
Điều kiện của m để phương trình có nghiệm là.
 Xem đáp án
Xem đáp án
Điều kiện có nghiệm của phương trình là: là
Chọn C
Câu 15:
Tìm tất cả các giá trị của tham số m để phương trình vô nghiệm?
 Xem đáp án
Xem đáp án
Ta có:
Điều kiện phương trình (1) vô nghiệm là: .
Vậy với thì phương trình trên vô nghiệm.
Chọn D
Câu 16:
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn để phương trình có nghiệm.
 Xem đáp án
Xem đáp án
Phương trình có nghiệm
Vì m nhận giá trị nguyên thuộc đoạn nên có 11 giá trị m thỏa mãn yêu cầu bài toán.
Chọn D
Câu 17:
Trong các phương trình sau phương trình nào có nghiệm:
 Xem đáp án
Xem đáp án
Chọn C
Phương trình có . Vậy phương trình có nghiệm.
Câu 22:
Nghiệm của phương trình lượng giác có nghiệm là:
 Xem đáp án
Xem đáp án
Chọn B
Ta có
Vì nên chỉ có thỏa mãn. Vậy ta có
Câu 23:
Nghiệm của phương trình thỏa điều kiện: .
 Xem đáp án
Xem đáp án
Chọn A
Vì nên nghiệm của phương trình là .
Câu 25:
Phương trình có bao nhiêu nghiệm trên khoảng ?
 Xem đáp án
Xem đáp án
Chọn A
PT đã cho .
Theo đề: .
Vì nên . Vậy PT đã cho có 5 nghiệm trên khoảng .
Câu 26:
Phương trình lượng giác có nghiệm là:
 Xem đáp án
Xem đáp án
Chọn A
Ta có Đặt với điều kiện ta được phương trình bậc hai theo t là
Phương trình có hai nghiệm và nhưng chỉ có thỏa mãn điều kiện. Vậy ta có
Câu 27:
Cho phương trình: . Bằng cách đặt thì phương trình trở thành phương trình nào sau đây?
 Xem đáp án
Xem đáp án
Chọn A
.
Câu 28:
Tìm tổng tất cả các nghiệm thuộc đoạn của phương trình .
 Xem đáp án
Xem đáp án
Chọn A
Ta có: , .
Theo đề bài:
Vậy tổng các nghiệm là: .
Câu 29:
Số nghiệm của phương trình trong là
 Xem đáp án
Xem đáp án
Chọn C
Ta có
Để .
Khi đó phương trình có 2018 nghiệm.
Vậy chọn đáp án C
Câu 30:
Tìm nghiệm của phương trình lượng giác thỏa mãn điều kiện .
 Xem đáp án
Xem đáp án
Chọn A.
Ta có .
Với , do nên ta được .
Với , do nên không có x nào thỏa mãn.
Câu 38:
Điều kiện có nghiệm của pt là
 Xem đáp án
Xem đáp án
Chọn A
Áp dụng công thức điều kiện để phương trình bậc nhất với sin và cos có nghiệm
Câu 39:
Trong các phương trình sau phương trình nào có nghiệm:
 Xem đáp án
Xem đáp án
Chọn C
Phương trình có . Vậy phương trình có nghiệm.
Câu 40:
Có bao nhiêu số nguyên m để phương trình có nghiệm?
 Xem đáp án
Xem đáp án
Chọn D
Phương trình có nghiệm khi và chỉ khi .
Suy ra có 27 số nguyên m để phương trình có nghiệm.
Câu 41:
Giá trị lớn nhất, nhỏ nhất của hàm số bằng a và b. Khi đó có giá trị bằng
 Xem đáp án
Xem đáp án
Chọn C
Ta có .
Gọi là một giá trị của hàm số khi đó phương trình có nghiệm khi và chỉ khi .
Suy ra Vậy
Câu 42:
Cho phương trình , với m là một phần tử của tập hợp . Có bao nhiêu giá trị của m để phương trình đã cho có nghiệm?
 Xem đáp án
Xem đáp án
Chọn A
Ta có
.
Phương trình trên có nghiệm khi và chỉ khi .
Vậy có ba giá trị của để phương trình đã cho có nghiệm.
Câu 43:
Số nghiệm thuộc của phương trình là:
 Xem đáp án
Xem đáp án
Chọn C
Ta có
Bài ra nên .
.
.
Do đó số nghiệm thuộc của phương trình đã cho là 2.
Câu 45:
Tìm giá trị nguyên lớn nhất của a để phương trình có nghiệm
 Xem đáp án
Xem đáp án
Chọn B
có nghiệm khi .
Do và là số lớn nhất nên .
Câu 47:
Tìm tất cả các giá trị của tham số m để phương trình có nghiệm.
 Xem đáp án
Xem đáp án
Chọn A
Điều kiện có nghiệm của phương trình là: .
Câu 49:
Tìm số các giá trị nguyên của m để phương trình có nghiệm.
 Xem đáp án
Xem đáp án
Chọn D
Phương trình có nghiệm khi và chỉ khi:
Vậy có 1 giá trị nguyên.
Câu 51:
Tính tổng tất cả các nghiệm thuộc khoảng của phương trình:
 Xem đáp án
Xem đáp án
Chọn C
Ta có: .
Vì nên nhận , , .
Câu 52:
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn để phương trình vô nghiệm.
 Xem đáp án
Xem đáp án
Chọn C
Phương trình vô nghiệm .
có 18 giá trị.
Câu 53:
Cho phương trình với m là tham số. Có bao nhiêu giá trị nguyên của m để phương trình có nghiệm?
 Xem đáp án
Xem đáp án
Chọn C
Điều kiện để phương trình có nghiệm là .
Vậy .
Câu 55:
Tìm tất cả các giá trị của tham số m sao cho phương trình vô nghiệm?
 Xem đáp án
Xem đáp án
Chọn D
Phương trình vô nghiệm khi
.
Câu 56:
Hàm số có tất cả bao nhiêu giá trị nguyên?
 Xem đáp án
Xem đáp án
Chọn B
Ta có .
Điều kiện để phương trình có nghiệm .
nên có 2 giá trị nguyênCâu 57:
Tổng tất cả các giá trị nguyên của m để phương trình có nghiệm là:
 Xem đáp án
Xem đáp án
Chọn A
.
Phương trình có nghiệm khi
Vì nên .
Vây tổng tất cả các giá trị nguyên của m để phương trình có nghiệm là .
Câu 59:
Với giá trị lớn nhất của a bằng bao nhiêu để phương trình có nghiệm?
 Xem đáp án
Xem đáp án
Chọn D
Ta có:
.
Phương trình có nghiệm .
Câu 61:
Tìm để phương trình có nghiệm
 Xem đáp án
Xem đáp án
Chọn A
Đặt , do suy ra .
Phương trình trở thành tìm m để phương trình có nghiệm thuộc đoạn .
Ta có ![]() .
.
Hoành độ đỉnh là loại. Ta có và .
Suy ra . Vậy ta chọn đáp án A.
Câu 62:
Tìm tất cả các giá trị của tham số m để phương trình vô nghiệm?
 Xem đáp án
Xem đáp án
Chọn D
Ta có:
Điều kiện phương trình vô nghiệm là: .
Vậy với thì phương trình trên vô nghiệm.
Câu 63:
Điều kiện để phương trình có nghiệm là:
 Xem đáp án
Xem đáp án
Chọn A
Điều kiện để phương trình có nghiệm là .
Câu 64:
Tìm m để phương trình có nghiệm.
 Xem đáp án
Xem đáp án
Chọn C
Ta có nên
(1)
Phương trình (1) có nghiệm khi và chỉ khi
Câu 65:
Để phương trình: có nghiệm, các giá trị thích hợp của tham số m là:
 Xem đáp án
Xem đáp án
Chọn B
Đặt
Để phương trình có nghiệm thì
Câu 66:
Cho phương trình:, trong đó m là tham số thựC. Để phương trình có nghiệm, các giá trị thích hợp của m là
 Xem đáp án
Xem đáp án
Chọn D
Đặt . Khi đó ta có phương trình
Phương trình đã cho có nghiệm khi phương trình có nghiệm
Câu 67:
 Xem đáp án
Xem đáp án
Lời giải. Ta có
Nhận thấy với nghiệm Chọn B
Câu 68:
 Xem đáp án
Xem đáp án
Với , suy ra . Chọn A
Cách 2. Thử lần lượt vào từng phương trình.
Câu 69:
 Xem đáp án
Xem đáp án
Ta có
TH1. Với
TH2. Với
So sánh hai nghiệm ta được là nghiệm dương nhỏ nhất. Chọn C
Câu 70:
 Xem đáp án
Xem đáp án
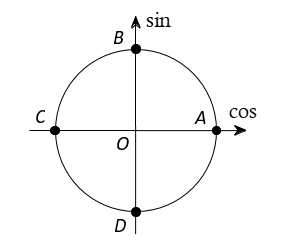
Quá dễ để nhận ra có 4 vị trí biểu diễn nghiệm của phương trình đã cho trên đường tròn lượng giác là A, B, C, D. Chọn A
Cách trắc nghiệm. Ta có có 4 vị trí biểu diễn.
Câu 71:
 Xem đáp án
Xem đáp án
Ta có
Theo giả thiết, ta có
. Vậy có tất cả 2018 giá trị nguyên của k tương ứng với có 2018 nghiệm thỏa mãn yêu cầu bài toán. Chọn D
Câu 72:
 Xem đáp án
Xem đáp án
Ta có . Mà
Do đó . Vậy Chọn D
Câu 73:
 Xem đáp án
Xem đáp án
Ta có
Vậy . Chọn B
Câu 74:
 Xem đáp án
Xem đáp án
Ta có .
= Với
= Với
Nhận thấy chưa có đáp án nào phù hợp. Ta biểu diễn các nghiệm trên đường tròn lượng giác (hình vẽ).
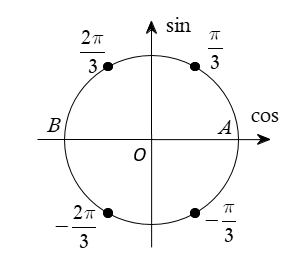
Nếu tính luôn hai điểm A, B thì có tất cả 6 điểm cách đều nhau nên ta gộp được 6 điểm này thành một họ nghiệm, đó là .
Suy ra nghiệm của phương trình Chọn D
Câu 75:
 Xem đáp án
Xem đáp án
Ta có . Chi hai vế phương trình cho ta được .
Chọn D
Câu 76:
 Xem đáp án
Xem đáp án
Phương trình
= Với .
có 6 nghiệm.
= Với .
có 6 nghiệm.
Vậy phương trình đã cho có 12 nghiệm. Chọn D
Câu 77:
 Xem đáp án
Xem đáp án
Ta có .
Phương trình có nghiệm
Vậy có tất cả 3 giá trị nguyên của tham số m. Chọn C
Câu 78:
 Xem đáp án
Xem đáp án
Ta có
Phương trình có nghiệm .
Vậy có tất cả 2018 giá trị nguyên của tham số m. Chọn A
Câu 79:
 Xem đáp án
Xem đáp án
Vì là một nghiệm của phương trình nên ta có:
.
Vậy là giá trị cần tìm. Chọn C
Câu 80:
 Xem đáp án
Xem đáp án
Để phương trình có nghiệm
là giá trị cần tìm. Chọn B
Câu 81:
 Xem đáp án
Xem đáp án
TH1. Với , phương trình : vô lý.
Suy ra thì phương trình đã cho vô nghiệm.
TH2. Với , phương trình
Để phương trình (*) vô nghiệm
Kết hợp hai trường hợp, ta được là giá trị cần tìm. Chọn D
Câu 82:
 Xem đáp án
Xem đáp án
Phương trình
Xét nghiệm , với ta được Chọn C
Câu 83:
 Xem đáp án
Xem đáp án
Phương trình
= không có giá trị k thỏa mãn.
= Chọn A
Câu 85:
 Xem đáp án
Xem đáp án
Phương trình
So sánh hai nghiệm ta được nghiệm dương nhỏ nhất là Chọn B
Cách trắc nghiệm. Thử từng nghiệm của đáp án vào phương trình và so sánh nghiệm nào thỏa mãn phương trình đồng thời là nhỏ nhất thì ta chọn.
Câu 86:
 Xem đáp án
Xem đáp án
Phương trình
=
=
Vậy có 4 nghiệm thỏa mãn. Chọn D
Câu 87:
 Xem đáp án
Xem đáp án
Ta có và .
Do đó phương trình
Xét nghiệm .
Vậy phương trình có nghiệm Chọn B
Câu 88:
 Xem đáp án
Xem đáp án
Phương trình
So sánh hai nghiệm ta được nghiệm âm lớn nhất của phương trình là Chọn A
Câu 89:
 Xem đáp án
Xem đáp án
Phương trình
Suy ra Chọn D
Câu 90:
 Xem đáp án
Xem đáp án
Điều kiện
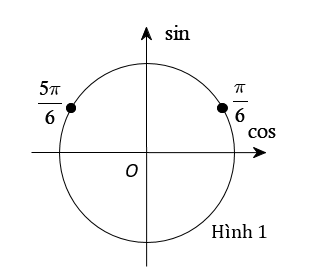
Điều kiện bài toán tương đương với bỏ đi vị trí hai điểm trên đường tròn lượng giác (Hình 1).
Phương trình
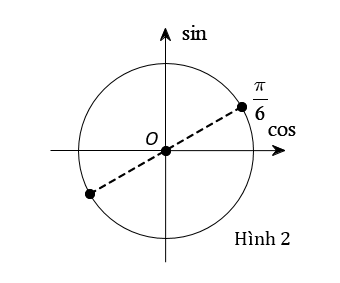
Biểu diễn nghiệm trên đường tròn lượng giác ta được 2 vị trí như Hình 2.
Đối chiếu điều kiện, ta loại nghiệm . Do đó phương trình có nghiệm Chọn C
Câu 91:
 Xem đáp án
Xem đáp án
Ta có
Điều kiện để phương trình có nghiệm
nên có 2 giá trị nguyên. Chọn B
Câu 92:
 Xem đáp án
Xem đáp án
Phương trình
.
Đặt
Phương trình trở thành
=
=
Suy ra nghiệm dương nhỏ nhất của phương trình là Chọn B
Câu 93:
 Xem đáp án
Xem đáp án
Phương trình vô nghiệm
có 18 giá trị. Chọn C
Câu 94:
 Xem đáp án
Xem đáp án
Phương trình vô nghiệm
Chọn D
Câu 95:
 Xem đáp án
Xem đáp án
Phương trình có nghiệm
có 18 giá trị. Chọn C
Câu 96:
 Xem đáp án
Xem đáp án
Phương trình
Phương trình có ng hiệm
có 2020 giá trị. Chọn D
Câu 97:
 Xem đáp án
Xem đáp án
Phương trình
Theo giả thiết
Vậy phương trình có duy nhất một nghiệm trên . Chọn A
Câu 98:
 Xem đáp án
Xem đáp án
Phương trình
Suy ra có duy nhất 1 vị trí biểu diễn nghiệm của phương trình trên đường tròn lượng giác. Chọn A
Câu 100:
 Xem đáp án
Xem đáp án
Phương trình
=
=
Vậy có tất cả 4 nghiệm thỏa mãn. Chọn B
Câu 101:
 Xem đáp án
Xem đáp án
Phương trình
Do
Vậy phương trình có 6 nghiệm thỏa mãn. Chọn C
Câu 103:
 Xem đáp án
Xem đáp án
Điều kiện:
Phương trình
Vậy phương trình đã cho có 2 nghiệm thỏa mãn. Chọn B
Câu 105:
 Xem đáp án
Xem đáp án
Phương trình
Suy ra có duy nhất 1 vị trí đường tròn lượng giác biểu diễn nghiệm. Chọn A
Câu 106:
 Xem đáp án
Xem đáp án
Ta có
Do đó phương trình
Đặt , phương trình trở thành Chọn A
Câu 107:
 Xem đáp án
Xem đáp án
Ta có .
Do đó phương trình
.
Ta có ; .
Vậy có hai nghiệm thỏa mãn. Chọn B
Câu 108:
 Xem đáp án
Xem đáp án
Phương trình .
Để phương trình đã cho có nghiệm khi và chỉ khi .
Chọn D
Câu 109:
 Xem đáp án
Xem đáp án
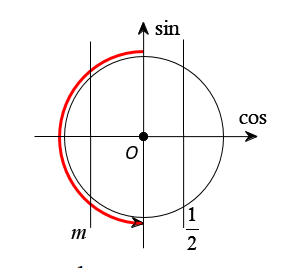
Nhận thấy phương trình không có nghiệm trên khoảng (Hình vẽ). Do đó yêu cầu bài toán có nghiệm thuộc khoảng .
Chọn B
Câu 110:
 Xem đáp án
Xem đáp án
Đặt .
Phương trình trở thành
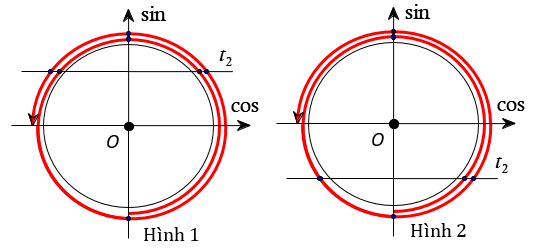
Yêu cầu bài toán tương đương với:
= TH1: Phương trình (*) có một nghiệm (có một nghiệm x) và một nghiệm (có bốn nghiệm x) (Hình 1).
a Do .
a Thay vào phương trình (*), ta được
= TH2: Phương trình (*) có một nghiệm (có hai nghiệm x) và một nghiệm (có ba nghiệm x) (Hình 2).
a Do .
a Thay vào phương trình (*) , ta được
Vậy thỏa mãn yêu cầu bài toán. Do Chọn D
Câu 111:
 Xem đáp án
Xem đáp án
Đặt . Phương trình trở thành
Ta có . Suy ra phương trình có hai nghiệm
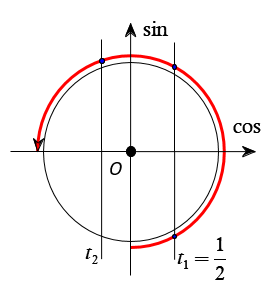
Ta thấy ứng với một nghiệm thì cho ta hai nghiệm x thuộc khoảng Do đó yêu cầu bài toán Chọn B
Cách 2. Yêu cầu bài toán tương đươn với phương trình có hai nghiệm thỏa mãn
Câu 113:
 Xem đáp án
Xem đáp án
Phương trình
=
=
Vậy tập nghiệm của phương trình chứa các nghiệm và . Chọn B
Câu 114:
 Xem đáp án
Xem đáp án
Phương trình
=
=
Vậy phương trình đã cho tương đương với . Chọn D
Câu 115:
 Xem đáp án
Xem đáp án
Phương trình
=
=
Ta có
Vậy phương trình đã cho tương đương với .Chọn B
Câu 116:
 Xem đáp án
Xem đáp án
Với Thay vào phương trình ta thấy thỏa mãn. Vậy A đúng.
= Phương trình
. Vậy B đúng.
= Phương trình
. Vậy C sai. Chọn C
= Phương trình Vậy D đúng.
Câu 117:
 Xem đáp án
Xem đáp án
Phương trình
có 2 vị trí biểu diễn nghiệm trên đường tròn lượng gác. Chọn C
Câu 118:
 Xem đáp án
Xem đáp án
Phương trình
Vì .
Vì
.
Vậy có tất cả 8 nghiệm. Chọn D
Câu 119:
 Xem đáp án
Xem đáp án
Phương trình
So sánh hai nghiệm ta được là nghiệm dương nhỏ nhất. Chọn B
Câu 121:
 Xem đáp án
Xem đáp án
Phương trình
So sánh hai nghiệm ta được là nghiệm âm lớn nhất. Chọn B
Câu 122:
 Xem đáp án
Xem đáp án
Phương trình
Phương trình có nghiệm
có 16 giá trị nguyên. Chọn A
Câu 123:
 Xem đáp án
Xem đáp án
Phương trình
Phương trình có nghiệm
có 2 giá trị nguyên. Chọn A
Câu 124:
 Xem đáp án
Xem đáp án
Phương trình .
Phương trình có nghiệm
Chọn C
Câu 125:
 Xem đáp án
Xem đáp án
Phương trình
Phương trình vô nghiệm Chọn B
Câu 126:
 Xem đáp án
Xem đáp án
Phương trình
.
Phương trình có nghiệm
có 6 giá trị nguyên. Chọn C
Câu 127:
 Xem đáp án
Xem đáp án
Đặt . Vì .
Ta có .
Khi đó, phương trình đã cho trở thành
Với , ta được .
. Chọn B
Câu 128:
 Xem đáp án
Xem đáp án
Đặt
Phương trình đã cho trở thành Chọn A
Câu 129:
 Xem đáp án
Xem đáp án
Đặt . Điều kiện
Ta có
Khi đó, phương trình đã cho trở thành : vô nghiệm.
Nhận thấy trong các đáp án A, B, C, D thì phương trình ở đáp án D vô nghiệm.
Vậy phương trình đã cho tương đương với phương trình Chọn D
Câu 130:
 Xem đáp án
Xem đáp án
Đặt . Điều kiện
Ta có
Phương trình đã cho trở thành
Với t=1, ta được
.
TH1. Với
TH2. Với
Vậy nghiệm âm lớn nhất của phương trình là . Chọn C
Câu 131:
 Xem đáp án
Xem đáp án
Đặt . Điều kiện
Ta có
Phương trình đã cho trở thành .
Với t=1, ta được
Với t=0, ta được
Chọn B
Câu 132:
 Xem đáp án
Xem đáp án
Đặt . Điều kiện
Ta có
Phương trình đã cho trở thành
Với (*)
Mặt khác , kết hợp với (*) suy ra
. Chọn D
Câu 133:
 Xem đáp án
Xem đáp án
Đặt . Điều kiện
Ta có
Phương trình đã cho trở thành
Chọn C
Câu 134:
 Xem đáp án
Xem đáp án
Đặt
Phương trình trở thành
Chọn C
Câu 138:
 Xem đáp án
Xem đáp án
Đặt . Vì .
Ta có
Phương trình đã cho trở thành
Với , ta được .
Theo giả thiết
có 4037 giá trị của k nê có 4037 nghiệm. Chọn A
Câu 139:
 Xem đáp án
Xem đáp án
Điều kiện .
Ta có
Đặt
Phương trình trở thành
Mà
. Chọn C
Câu 140:
 Xem đáp án
Xem đáp án
Phương trình
Đặt
Phương trình trở thành
Với , ta được .
Mà Chọn D
Câu 141:
 Xem đáp án
Xem đáp án
Đặt
Phương trình trở thành .
Do .
Vậy để phương trình có nghiệm
Chọn C
