Đề kiểm tra Giữa kì 2 Toán 11 KNTT có đáp án - Đề 01
-
48 lượt thi
-
38 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Cho $a$ là số thực dương, $m \in \mathbb{Z},n \in \mathbb{N},n \geqslant 2.$ Khẳng định nào sau đây sai?
Xem đáp án
Chọn C
Câu 2:
Cho \[x,y\] là hai số thực dương khác \[1\] và \[n,m\] là hai số thực tùy ý.
Đẳng thức nào sau đây sai?
Xem đáp án
Chọn C
Câu 4:
Rút gọn biểu thức $P = \sqrt[3]{{\sqrt {{a^{12}}{b^{18}}} }}\left( {a > 0,b > 0} \right)$ thu được kết quả là
Xem đáp án
Chọn A
Câu 8:
Với mọi $a$, $b$, $x$ là các số thực dương thoả mãn $\log { & _2}x = 5{\log _2}a + 3{\log _2}b$.
Mệnh đề nào dưới đây đúng?
Xem đáp án
Chọn C
Câu 14:
Tìm tập nghiệm $S$ của bất phương trình ${\log _{\frac{1}{2}}}\left( {x + 1} \right) < {\log _{\frac{1}{2}}}\left( {2x - 1} \right)$.
Xem đáp án
Chọn D
Câu 17:
Cho hình lập phương $ABCD.A'B'C'D'$. Góc giữa hai đường thẳng $AC$ và $AA'$ là góc nào sau đây?
Xem đáp án
Chọn D
Câu 18:
Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$ và các cạnh bên đều bằng $a$. Gọi $M$ và $N$ lần lượt là trung điểm của cạnh $AD,\,\,SD$. Khẳng định nào sau đây đúng?
Xem đáp án
Chọn A
Câu 19:
Qua điểm \[O\] cho trước, có bao nhiêu mặt phẳng vuông góc với đường thẳng $\Delta $ cho trước?
Xem đáp án
Chọn A
Câu 20:
Cho tứ diện $OABC$ có $OA,\,OB,\,OC$ đôi một vuông góc với nhau Mệnh đề nào dưới đây đúng?
Xem đáp án
Chọn A
Câu 21:
Cho hình lập phương $ABCD.A'B'C'D'$. Đường thẳng $AC'$ vuông góc với mặt phẳng nào sau đây?
Xem đáp án
Chọn A
Câu 23:
Cho hình chóp $S.ABC$ có $SC$ vuông góc với $\left( {ABC} \right)$. Góc giữa $SA$ với $\left( {ABC} \right)$ là góc giữa
Xem đáp án
Chọn D
Câu 24:
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông, \[SA\] vuông góc với mặt phẳng \[\left( {ABCD} \right)\]. Chọn khẳng định sai?
Xem đáp án
Chọn B
Câu 27:
Trong không gian cho hình hộp chữ nhật $ABCD.A'B'C'D'$, mặt phẳng nào sau đây vuông góc với mặt phẳng $\left( {ABCD} \right)$ ?
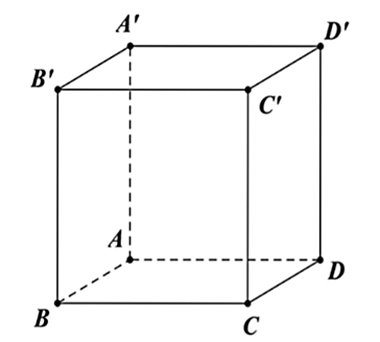
Xem đáp án
Chọn A
Câu 28:
Cho hình chóp \[S.ABCD\] có \[SA \bot \left( {ABCD} \right)\] đáy \[ABCD\] là hình thoi cạnh $a$ và $AC = a$. Số đo góc nhị diện \[\left[ {B,SA,D} \right]\] bằng
Xem đáp án
Chọn C
Câu 31:
Cho hình chóp tứ giác đều $S.ABCD$ có \[AB = SA = 2a\]. Khoảng cách từ đường thẳng $AD$ đến mặt phẳng \[\left( {SBC} \right)\] bằng
Xem đáp án
Chọn B
Câu 33:
Cho khối chóp có đáy là hình vuông cạnh $a$ và chiều cao bằng $2a$. Thể tích của khối chóp đã cho bằng
Xem đáp án
Chọn B
Câu 35:
Cho khối chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \[a\], tam giác \[SAB\] cân tại \[S\] và nằm trong mặt phẳng vuông góc với mặt đáy, \[SA = 2a\]. Tính theo $a$ thể tích $V$ của khối chóp \[S.ABCD\] ta được
Xem đáp án
Chọn B
Câu 36:
a) Biết ${\log _x}y = 2$. Tính giá trị của ${\log _{{x^2}y}}\frac{{{x^4}}}{{y\sqrt y }}$.
b) Tìm $m$ nguyên để hàm số \[f\left( x \right) = {\left( {2{x^2} + mx + 2} \right)^{\frac{3}{2}}}\] xác định với mọi $x \in \mathbb{R}$.
Xem đáp án
a) (0,5 điểm)
Ta có ${\log _x}y = 2 \Rightarrow y = {x^2};\,\,x,\,y > 0,\,x \ne 1$.
Vậy ${\log _{{x^2}y}}\frac{{{x^4}}}{{y\sqrt y }} = {\log _{{x^4}}}\frac{{{x^4}}}{{{x^3}}} = {\log _{{x^4}}}x = \frac{1}{4}$.
b) (0,5 điểm)
Hàm số \[f\left( x \right) = {\left( {2{x^2} + mx + 2} \right)^{\frac{3}{2}}}\] xác định với mọi $x \in \mathbb{R}$
$ \Leftrightarrow 2{x^2} + mx + 2 > 0,x \in \mathbb{R}$
$ \Leftrightarrow \Delta < 0 \Leftrightarrow {m^2} - 16 < 0$$ \Leftrightarrow - 4 < m < 4$.
Vì $m$ nguyên nên \[m \in \left\{ { - 3\,; - 2\,; - 1\,;0\,;1\,;2\,;3} \right\}\].
Vậy có tất cả \[7\] giá trị $m$ thỏa mãn điều kiện đề bài.
Câu 37:
Cho hình chóp \[S.ABC\] có đáy là tam giác \[ABC\] vuông cân tại \[B\], \[SA \bot \left( {ABC} \right)\]. Gọi \[H\] là hình chiếu của \[A\] lên \[SB\].
a) Chứng minh rằng \[AH \bot \left( {SBC} \right)\].
b) Tính góc giữa hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {SBC} \right)\], biết \[SA = AB = a\].
Xem đáp án
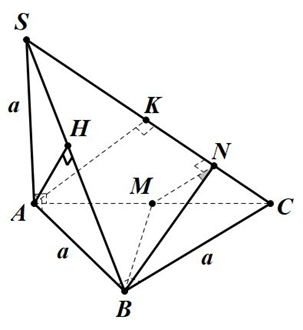
a) Ta có \[\left\{ \begin{gathered}
BC \bot SA \hfill \\
BC \bot AB \hfill \\
\end{gathered} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AH\].
Ta lại có \[\left\{ \begin{gathered}
AH \bot SB \hfill \\
AH \bot BC \hfill \\
\end{gathered} \right. \Rightarrow AH \bot \left( {SBC} \right)\].
b) Gọi \[M\] là trung điểm của \[AC\] và \[N\] là hình chiếu của \[M\] trên \[SC\].
Ta có \[MB \bot AC \Rightarrow MB \bot \left( {SAC} \right) \Rightarrow MB \bot SC\].
Từ đó suy ra $SC \bot \left( {MNB} \right)$ nên $SC \bot MN$.
Do đó \[\left( {\left( {SAC} \right),\left( {SBC} \right)} \right) = \widehat {MNB}\].
Gọi \[K\] là hình chiếu của \[A\] lên \[SC\].
Ta tính được \[MB = \frac{{a\sqrt 2 }}{2}\]; \[AK = \frac{{SA \cdot AC}}{{SC}} = \frac{{a\sqrt 6 }}{3} \Rightarrow MN = \frac{{a\sqrt 6 }}{6}\].
Ta có \[\tan \widehat {MNB} = \frac{{MB}}{{MN}} = \frac{{\frac{{a\sqrt 2 }}{2}}}{{\frac{{a\sqrt 6 }}{6}}} = \sqrt 3 \Rightarrow \widehat {MNB} = 60^\circ \].
Vậy góc giữa hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {SBC} \right)\] bằng \[60^\circ \].
Câu 38:
Cho hình chóp \[S.ABCD\] có đáy là hình chữ nhật với \[AB = a,BC = a\sqrt 3 \]. Hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {SBD} \right)\] cùng vuông góc với đáy. Điểm \[I\] thuộc đoạn \[SC\] sao cho \[SC = 3IC\]. Tính khoảng cách giữa hai đường thẳng \[AI\] và \[SB\] biết rằng \[AI\] vuông góc với \[SC\].
Xem đáp án
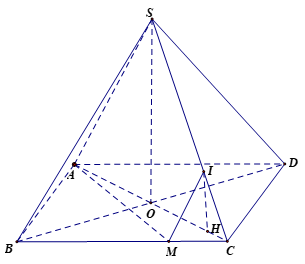
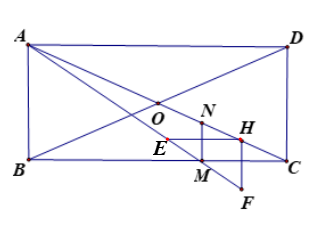
Gọi \[O\] là tâm hình chữ nhật \[ABCD\], \[(SAC) \cap (SBD) = SO\] suy ra \[SO \bot \left( {ABCD} \right)\].
Ta có \[AC = \sqrt {A{B^2} + B{C^2}} = 2a \Rightarrow OC = a\].
Mà .
Kẻ \[IM{\text{//}}SB\left( {M \in BC} \right) \Rightarrow SB{\text{//}}\left( {AIM} \right)\], suy ra
\[d\left( {SB,AI} \right) = d\left( {SB,\left( {AIM} \right)} \right) = d\left( {B,\left( {AIM} \right)} \right)\].
Kẻ \[IH{\text{//}}SO\left( {H \in OC} \right) \Rightarrow IH \bot \left( {ABCD} \right)\] và \[\frac{{HC}}{{OC}} = \frac{{IC}}{{SC}} = \frac{1}{3}\].
Ta có \[d\left( {B,\left( {AIM} \right)} \right) = 2d\left( {C,\left( {AIM} \right)} \right) = 2 \cdot \frac{6}{5}d\left( {H,\left( {AIM} \right)} \right) = \frac{{12}}{5}h\].
Kẻ \[HE{\text{//}}AD,HF{\text{//}}DC{\text{ }}\left( {E,F \in AM} \right) \Rightarrow HE \bot HF\] mà $IH \bot \left( {HEF} \right)$ nên \[H.IEF\] là tứ diện vuông tại \[H\].
Ta có \[\frac{1}{{{h^2}}} = \frac{1}{{H{I^2}}} + \frac{1}{{H{E^2}}} + \frac{1}{{H{F^2}}}\]
với $IH = \frac{1}{3}SO = \frac{{a\sqrt 5 }}{3}$; \[HE = \frac{5}{6}MC = \frac{5}{6} \cdot \frac{1}{3}BC = \frac{{5a\sqrt 3 }}{{18}};\]\[HF = \frac{5}{4}MN = \frac{5}{4}.\frac{1}{3}AB = \frac{5}{{12}}a\].
Suy ra \[\frac{1}{{{h^2}}} = \frac{1}{{H{I^2}}} + \frac{1}{{H{E^2}}} + \frac{1}{{H{F^2}}} = \frac{{297}}{{25{a^2}}} \Rightarrow h = \frac{{5a}}{{3\sqrt {33} }}\].
Vậy ta có \[d\left( {AI,SB} \right) = \frac{{12}}{5} \cdot \frac{{5a}}{{3\sqrt {33} }} = \frac{{4a}}{{\sqrt {33} }}\].