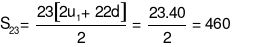20 câu trắc nghiệm Toán 11 KNTT Bài 6. Cấp số cộng có đáp án
-
72 lượt thi
-
20 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho cấp số cộng (un) với số hạng đầu u1 và công sai d. Số hạng tổng quát của cấp số cộng đã cho được tính theo công thức nào dưới đây ?
 Xem đáp án
Xem đáp án
Theo định lí ta có công thức số hạng tổng quát của cấp số cộng là: 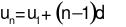
Đáp án cần chọn là: D
Câu 2:
Cho cấp số cộng (un) với số hạng đầu u1 và công sai . Tổng n số hạng đầu tiên của cấp số cộng đã cho được tính theo công thức nào dưới đây ?
 Xem đáp án
Xem đáp án
Theo định lí ta có công thức tính tổng n số hạng đầu tiên của cấp số cộng là:
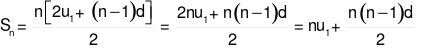
Đáp án cần chọn là:
ACâu 3:
Trong các dãy số (un) cho bởi số hạng tổng quát un sau, dãy số nào là một cấp số cộng:
 Xem đáp án
Xem đáp án
Xét đáp án A. Dãy số là cấp số cộng với công sai d = −4.
Xét đáp án B. Vì 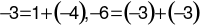 nên dãy số không là cấp số cộng.
nên dãy số không là cấp số cộng.
Xét đáp án C. Vì 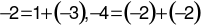 nên dãy số không là cấp số cộng.
nên dãy số không là cấp số cộng.
Xét đáp án D. Vì  nên dãy số không là cấp số cộng.
nên dãy số không là cấp số cộng.
Đáp án cần chọn là: A
Câu 4:
Cho cấp số cộng (un) với 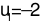 và
và 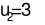 . Công sai của cấp số cộng đã cho bằng:
. Công sai của cấp số cộng đã cho bằng:
 Xem đáp án
Xem đáp án
Ta có: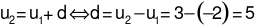
Đáp án cần chọn là: A
Câu 5:
Trong các dãy số (un) cho bởi số hạng tổng quát un sau, dãy số nào không phải là một cấp số cộng:
 Xem đáp án
Xem đáp án
Xét đáp A. Ta có: 
Xét hiệu: 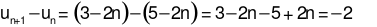
Vậy dãy số là cấp số cộng có công sai d = −2.
Xét đáp B. Ta có:
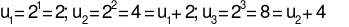
Vậy dãy số không là cấp số cộng.
Xét đáp C. Ta có: 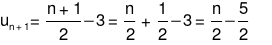
Xét hiệu: 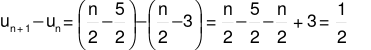
Vậy dãy số là cấp số cộng có công sai 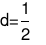
Xét đáp D. Ta có: 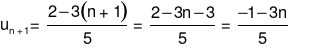 Xét hiệu:
Xét hiệu: 
Vậy dãy số là cấp số cộng có công sai
Đáp án cần chọn là: B
Câu 7:
Cho cấp số cộng (un) có số hạng đầu u1 = 2 và công sai d = −3. Tổng của 10 số hạng đầu tiên của cấp số cộng đã cho bằng:
 Xem đáp án
Xem đáp án
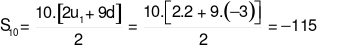
Đáp án cần chọn là:
ACâu 8:
Cho cấp số cộng (un), biết 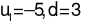 . Số 100 là số hạng thứ bao nhiêu?
. Số 100 là số hạng thứ bao nhiêu?
 Xem đáp án
Xem đáp án
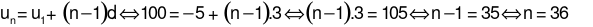
Đáp án cần chọn là:
DCâu 9:
Cho cấp số cộng (un) có d = −2 và , khi đó số hạng đầu tiên là bao nhiêu?
 Xem đáp án
Xem đáp án
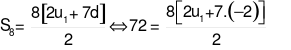
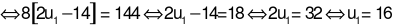
Đáp án cần chọn là:
C
Câu 10:
Cho cấp số cộng (un)có: 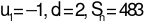 . Hỏi cấp số cộng có bao nhiêu số hạng?
. Hỏi cấp số cộng có bao nhiêu số hạng?
 Xem đáp án
Xem đáp án
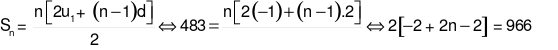
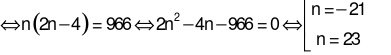
Vì 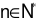 nên n = 23
nên n = 23
Đáp án cần chọn là: D
Câu 11:
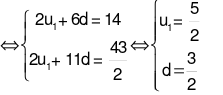
Cho cấp số cộng có 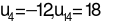 . Khi đó số hạng đầu tiên và công sai là:
. Khi đó số hạng đầu tiên và công sai là:
 Xem đáp án
Xem đáp án
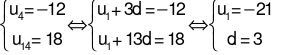
Đáp án cần chọn là:
BCâu 14:
Xen giữa các số 2 và 22 ba số nào sau đây để được một cấp số cộng có 5 số hạng.
 Xem đáp án
Xem đáp án
Giả sử cấp số cộng gồm 5 số hạng  .
.
Theo đề bài ta có 

Vậy ta cần viết thêm các số: 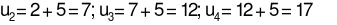 Đáp án cần chọn là: B
Đáp án cần chọn là: B
Câu 15:
Cho cấp số cộng (un) biết:  . Chọn đáp án đúng.
. Chọn đáp án đúng.
 Xem đáp án
Xem đáp án
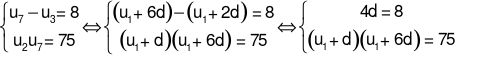
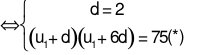
Thế
d = 2 vào (*) ta được: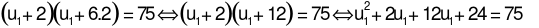
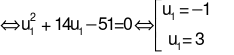
Đáp án cần chọn là:
CCâu 16:
Tìm công sai của cấp số cộng sau: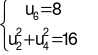 , biết công sai không lớn hơn 2.
, biết công sai không lớn hơn 2.
 Xem đáp án
Xem đáp án
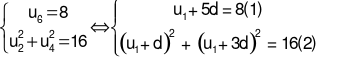
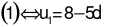 thế vào (2) ta được
thế vào (2) ta được
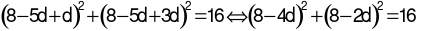
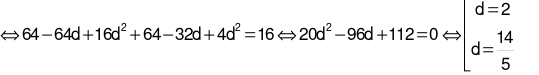
Vì công sai không lớn hơn 2 nên d = 2
Đáp án cần chọn là: B
Câu 17:
Ông Sơn trồng cây trên một mãnh đất hình tam giác theo quy luật: ở hàng thứ nhất có 1 cây, ở hàng thứ hai có 2 cây, ở hàng thứ ba có 3 cây,…, ở hàng thứ n có n cây. Biết rằng ông đã trồng hết 11325 cây. Hỏi số hàng cây được trồng theo cách trên là bao nhiêu?
 Xem đáp án
Xem đáp án
Theo đề bài ta có dãy số chỉ số cây trồng mỗi hàng là một cấp số cộng có số hạng đầu u1 = 1 và công sai d = 1.
Ông Sơn đã trồng hết 11325 cây nên ta có:
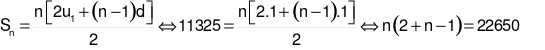
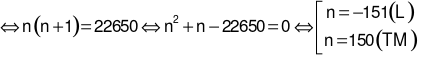
Vậy có 150 hàng cây được trồng theo cách trên.
Đáp án cần chọn là: B
Câu 19:
Cho miếng giấy hình tam giác ABC. Cắt tam giác này dọc theo ba đường trung bình của nó ta thu được 4 tam giác mới, gọi số tam giác có được là T1. Chọn 1 trong 4 tam giác được tạo thành và cắt nó theo ba đường trung bình, số tam giác vừa nhận được do việc cắt T1 là T2… Lặp lại quá trình này ta nhận được một dãy vô hạn các tam giác 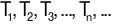 Hãy tính tổng 100 số hạng đầu tiên của dãy số (Tn).
Hãy tính tổng 100 số hạng đầu tiên của dãy số (Tn).
 Xem đáp án
Xem đáp án
Ở lần cắt đầu tiên có  tam giác.
tam giác.
Ở lần cắt thứ hai có  tam giác được giữ nguyên và có thêm 4 tam giác được tạo thành. Vậy ở lần cắt thứ hai có
tam giác được giữ nguyên và có thêm 4 tam giác được tạo thành. Vậy ở lần cắt thứ hai có 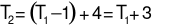 tam giác.
tam giác.
Ở lần cắt thứ ba có 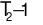 tam giác được giữ nguyên và có thêm 4 tam giác được tạo thành. Vậy ở lần cắt thứ ba có
tam giác được giữ nguyên và có thêm 4 tam giác được tạo thành. Vậy ở lần cắt thứ ba có 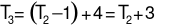 tam giác.
tam giác.
…
Ở lần cắt thứ n có  tam giác được giữ nguyên và có thêm 4 tam giác được tạo thành. Vậy ở lần cắt thứ n có
tam giác được giữ nguyên và có thêm 4 tam giác được tạo thành. Vậy ở lần cắt thứ n có  tam giác.
tam giác.
Vậy dãy số (Tn) là một cấp số cộng có số hạng đầu  và công sai d = 3.
và công sai d = 3.
Tổng 100 số hạng đầu tiên của dãy số (Tn) là:
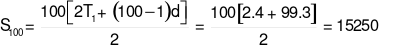
Đáp án cần chọn là: C
Câu 20:
Cho một cấp số cộng 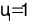 , tổng 100 số hạng đầu bằng 24850. Tính
, tổng 100 số hạng đầu bằng 24850. Tính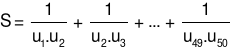
 Xem đáp án
Xem đáp án
Tổng 100 số hạng đầu bằng 24850 nên ta có:
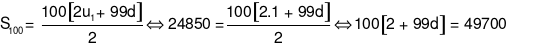
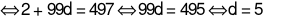
Ta có: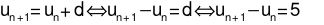

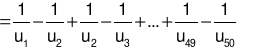
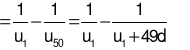
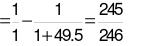
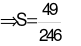
Đáp án cần chọn là:
B
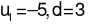 . Chọn đáp án đúng.
. Chọn đáp án đúng.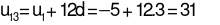
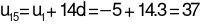

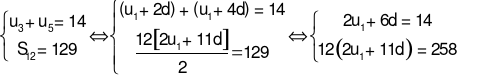

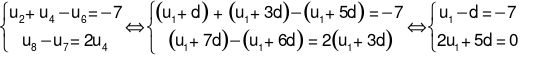
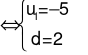
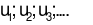 có công sai d. Biết . Tính S23.
có công sai d. Biết . Tính S23.