Giải SGK Toán 11 Cánh Diều Bài Các phép biến đổi lượng giác
-
681 lượt thi
-
27 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Ở lớp dưới, ta đã làm quen với một số phép tính trong tập hợp các số thực, chẳng hạn: phép tính luỹ thừa với số mũ tự nhiên và những công thức để tính toán hay biến đổi những biểu thức chứa các luỹ thừa như vậy. Việc lấy các giá trị lượng giác của góc lượng giác đã hình thành nên những phép tính mới trong tập hợp các số thực, đó là những phép tính lượng giác.

Có hay không những công thức để tính toán hay biến đổi những biểu thức chứa giá trị lượng giác?
 Xem đáp án
Xem đáp án
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Có các công thức để tính toán hay biến đổi những biểu thức chứa giá trị lượng giác sau:
‒ Công thức cộng;
‒ Công thức nhân đôi;
‒ Công thức biến đổi tích thành tổng;
‒ Công thức biến đổi tổng thành tích.
Câu 2:
Cho \(a = \frac{\pi }{6},b = \frac{\pi }{3}\). Hãy tính sina, cosa, sinb, cosb và sin(a + b). Từ đó rút ra đẳng thức sin(a + b) = sina cosb + cosa sinb (*).
 Xem đáp án
Xem đáp án
Với \(a = \frac{\pi }{6}\) ta có \[\sin a = \sin \frac{\pi }{6} = \frac{1}{2}\]; \(\cos a = \cos \frac{\pi }{6} = \frac{{\sqrt 3 }}{2}\).
Với \(b = \frac{\pi }{3}\) ta có \[\sin b = \sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\]; \(\cos b = \cos \frac{\pi }{3} = \frac{1}{2}\).
Ta có \(\sin \left( {a + b} \right) = \sin \left( {\frac{\pi }{6} + \frac{\pi }{3}} \right) = \sin \frac{\pi }{2} = 1\);
\[\sin a\cos b + \cos a\sin b = \frac{1}{2}.\frac{1}{2} + \frac{{\sqrt 3 }}{2}.\frac{{\sqrt 3 }}{2} = \frac{1}{4} + \frac{3}{4} = 1\]
Do đó sin(a + b) = sina cosb + cosa sinb (vì cùng bằng 1).
Câu 3:
Tính sin(a – b) bằng cách biến đổi sin(a – b) = sin[a + (‒b)] và sử dụng công thức (*).
 Xem đáp án
Xem đáp án
Ta có sin(a – b) = sin[a + (‒b)]
= sina cos(‒b) + cosa sin(‒b)
= sina cosb + cosa (‒sinb)
= sina cosb ‒ cosa sinb
Câu 4:
Tính \[\sin \frac{\pi }{{12}}\].
 Xem đáp án
Xem đáp án
Áp dụng công thức cộng ta có:
\[\sin \frac{\pi }{{12}} = \sin \left( {\frac{\pi }{3} - \frac{\pi }{4}} \right) = \sin \frac{\pi }{3}\cos \frac{\pi }{4} - \cos \frac{\pi }{3}\sin \frac{\pi }{4}\]
\( = \frac{{\sqrt 3 }}{2}.\frac{{\sqrt 2 }}{2} - \frac{1}{2}.\frac{{\sqrt 2 }}{2} = \frac{{\sqrt 6 - \sqrt 2 }}{4}\).
Câu 5:
Tính cos(a + b) bằng cách biến đổi cos(a + b) = \(\sin \left[ {\frac{\pi }{2} - \left( {a + b} \right)} \right] = \sin \left[ {\left( {\frac{\pi }{2} - a} \right) - b} \right]\) và sử dụng công thức cộng đối với sin.
 Xem đáp án
Xem đáp án
Ta có: cos(a + b) = \(\sin \left[ {\frac{\pi }{2} - \left( {a + b} \right)} \right] = \sin \left[ {\left( {\frac{\pi }{2} - a} \right) - b} \right]\)
\( = \sin \left( {\frac{\pi }{2} - a} \right).\cos b - c{\rm{os}}\left( {\frac{\pi }{2} - a} \right).\sin b\)
\( = \cos a.\cos b - \sin a.\sin b\)
Vậy cos(a + b) = cosa cosb – sina sinb.
Câu 6:
Tính cos(a ‒ b) bằng cách biến đổi cos(a – b) = cos[a + (‒b)] và sử dụng công thức cos(a + b) có được ở câu a.
 Xem đáp án
Xem đáp án
Ta có: cos(a – b) = cos[a + (‒b)]
= cosa cos(‒b) – sina sin(‒b)
= cosa cosb ‒ sina (‒sinb)
= cosa cosb + sina sinb.
Vậy cos(a – b) = cosa cosb + sina sinb.
Câu 7:
Tính cos15°.
 Xem đáp án
Xem đáp án
Áp dụng công thức cộng, ta có:
cos15° = cos(45° ‒ 30°)
= cos45°.cos30° + sin45°.sin30°
\( = \frac{{\sqrt 2 }}{2}.\frac{{\sqrt 3 }}{2} + \frac{{\sqrt 2 }}{2}.\frac{1}{2} = \frac{{\sqrt 6 + \sqrt 2 }}{4}\).
Câu 8:
Sử dụng công thức cộng đối với sin và côsin, hãy tính tan(a + b) theo tana và tanb khi các biểu thức đều có nghĩa.
 Xem đáp án
Xem đáp án
Khi các biểu thức đều có nghĩa, ta có:
tan(a + b) \( = \frac{{\sin \left( {a + b} \right)}}{{cos\left( {a + b} \right)}} = \frac{{\sin a\cos b + \cos a\sin b}}{{\cos a\cos b - \sin a\sin b}}\)
\[ = \frac{{\frac{{\sin a\cos b + \cos a\sin b}}{{\cos a\cos b}}}}{{\frac{{\cos a\cos b - \sin a\sin b}}{{\cos a\cos b}}}}\] (chia cả tử và mẫu cho cosacosb)
\[ = \frac{{\frac{{\sin a\cos b}}{{\cos a\cos b}} + \frac{{\cos a\sin b}}{{\cos a\cos b}}}}{{\frac{{\cos a\cos b}}{{\cos a\cos b}} - \frac{{\sin a\sin b}}{{\cos a\cos b}}}}\]
\[ = \frac{{\frac{{\sin a}}{{\cos a}} + \frac{{\sin b}}{{\cos b}}}}{{1 - \frac{{\sin a}}{{\cos a}}.\frac{{\sin b}}{{\cos b}}}}\]
\[ = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\]
Vậy \[\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\].
Câu 9:
Khi các biểu thức đều có nghĩa, hãy tính tan (a – b) bằng cách biến đổi \[tan\left( {a - b} \right) = tan\left[ {a + \left( { - b} \right)} \right]\] và sử dụng công thức tan(a + b) có được ở bài trước
 Xem đáp án
Xem đáp án
Khi các biểu thức đều có nghĩa, ta có:
\[tan\left( {a - b} \right) = tan\left[ {a + \left( { - b} \right)} \right]\]
\[ = \frac{{\tan a + \tan \left( { - b} \right)}}{{1 - \tan a\tan \left( { - b} \right)}}\]
\[ = \frac{{\tan a - \tan b}}{{1 + \tan a\tan b}}\].
Vậy \[\tan \left( {a - b} \right) = \frac{{\tan a - \tan b}}{{1 + \tan a\tan b}}\].
Câu 10:
Tính tan165°.
 Xem đáp án
Xem đáp án
Áp dụng công thức cộng, ta có:
tan165° = tan(120° + 45°)
\[ = \frac{{\tan 120^\circ + \tan 45^\circ }}{{1 - \tan 120^\circ \tan 45^\circ }}\]
\[ = \frac{{ - \sqrt 3 + 1}}{{1 - \left( { - \sqrt 3 } \right).1}} = \frac{{1 - \sqrt 3 }}{{1 + \sqrt 3 }} = \frac{{{{\left( {1 - \sqrt 3 } \right)}^2}}}{{\left( {1 + \sqrt 3 } \right)\left( {1 - \sqrt 3 } \right)}}\]
\( = \frac{{1 - 2\sqrt 3 + 3}}{{1 - 3}} = \frac{{4 - 1\sqrt 3 }}{{ - 2}} = - 2 + \sqrt 3 \).
Vậy \(\tan 165^\circ = - 2 + \sqrt 3 \).
Câu 11:
Tính sin2a, cos2a, tan2a bằng cách thay b = a trong công thức cộng.
 Xem đáp án
Xem đáp án
Ta có:
• sin2a = sin(a + a) = sinacosa + cosasina = 2sinacosa;
• cos2a = cos(a + a) = cosacosa – sinasina = cos2a – sin2a;
• Khi các biểu thức đều có nghĩa thì
\[\tan 2a = \tan \left( {a + a} \right) = \frac{{\tan a + \tan a}}{{1 - \tan a\tan a}} = \frac{{2\tan a}}{{1 - {{\tan }^2}a}}\].
Câu 12:
Cho \(\tan \frac{a}{2} = - 2\). Tính tana.
 Xem đáp án
Xem đáp án
Áp dụng công thức nhân đôi, ta có:
\[\tan a = \frac{{2\tan \frac{a}{2}}}{{1 - {{\tan }^2}\frac{a}{2}}} = \frac{{2.\left( { - 2} \right)}}{{1 - {{\left( { - 2} \right)}^2}}} = \frac{{ - 4}}{{ - 3}} = \frac{4}{3}\].
Câu 13:
Tính: \(\sin \frac{\pi }{8},\cos \frac{\pi }{8}\).
 Xem đáp án
Xem đáp án
Áp dụng công thức hạ bậc, ta có:
• \({\sin ^2}\frac{\pi }{8} = \frac{{1 - cos\left( {2.\frac{\pi }{8}} \right)}}{2} = \frac{{1 - \cos \frac{\pi }{4}}}{2} = \frac{{1 - \frac{{\sqrt 2 }}{2}}}{2} = \frac{{2 - \sqrt 2 }}{4}\)
Mà \(\sin \frac{\pi }{8} > 0\) nên \(\sin \frac{\pi }{8} = \sqrt {\frac{{2 - \sqrt 2 }}{4}} = \frac{{\sqrt {2 - \sqrt 2 } }}{2}\).
• \({\cos ^2}\frac{\pi }{8} = \frac{{1 + cos\left( {2.\frac{\pi }{8}} \right)}}{2} = \frac{{1 + \cos \frac{\pi }{4}}}{2} = \frac{{1 + \frac{{\sqrt 2 }}{2}}}{2} = \frac{{2 + \sqrt 2 }}{4}\)
Mà \(\cos \frac{\pi }{8} > 0\) nên \(\cos \frac{\pi }{8} = \sqrt {\frac{{2 + \sqrt 2 }}{4}} = \frac{{\sqrt {2 + \sqrt 2 } }}{2}\).
Câu 14:
Sử dụng công thức cộng, rút gọn mỗi biểu thức sau:
cos(a + b) + cos(a – b); cos(a + b) – cos(a – b); sin(a + b) + sin(a – b).
 Xem đáp án
Xem đáp án
Ta có:
• cos(a + b) + cos(a – b)
= (cosa cosb – sina sinb) + (cosa cosb + sina sinb)
= cosa cosb – sina sinb + cosa cosb + sina sinb
= 2cosa cosb.
• cos(a + b) – cos(a – b)
= (cosa cosb – sina sinb) – (cosa cosb + sina sinb)
= cosa cosb – sina sinb – cosa cosb – sina sinb
= –2sina sinb.
• sin(a + b) + sin(a – b)
= (sina cosb + cosa sinb) + (sina cosb ‒ cosa sinb)
= sina cosb + cosa sinb + sina cosb ‒ cosa sinb
= 2sina cosb.
Vậy cos(a + b) + cos(a – b) = 2cosa cosb;
cos(a + b) – cos(a – b) = –2sina sinb;
sin(a + b) + sin(a – b) = 2sina cosb.
Câu 15:
Cho \(\cos a = \frac{2}{3}\). Tính \(B = \cos \frac{{3a}}{2}\cos \frac{a}{2}\).
 Xem đáp án
Xem đáp án
Áp dụng công thức biến đổi tích thành tổng, ta có:
\(B = \cos \frac{{3a}}{2}\cos \frac{a}{2}\)
\( = \frac{1}{2}\left[ {\cos \left( {\frac{{3a}}{2} + \frac{a}{2}} \right) + \cos \left( {\frac{{3a}}{2} - \frac{a}{2}} \right)} \right]\)
\( = \frac{1}{2}\left[ {\cos 2a + \cos a} \right]\)
Mà cos2a = 2cos2a – 1 = \(2.{\left( {\frac{2}{3}} \right)^2} - 1 = 2.\frac{4}{9} - 1 = - \frac{1}{9}\)
Do đó \(B = \frac{1}{2}\left[ {\cos 2a + \cos a} \right] = \frac{1}{2}.\left[ { - \frac{1}{9} + \frac{2}{3}} \right] = \frac{5}{{18}}\).
Câu 16:
Sử dụng công thức biến đổi tích thành tổng và đặt a + b = u; a − b = v rồi biến đổi các biểu thức sau thành tích: cosu + cosv; cosu – cos v; sinu + sinv; sinu – sinv.
 Xem đáp án
Xem đáp án
Ta có \(\left\{ \begin{array}{l}a + b = u\\a - b = v\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{u + v}}{2}\\b = \frac{{u - v}}{2}\end{array} \right.\).
Khi đó:
• cosu + cosv = cos(a + b) + cos(a – b)
= 2cosa cosb
\( = 2\cos \frac{{u + v}}{2}\cos \frac{{u - v}}{2}\).
• cosu – cosv = cos(a + b) – cos(a – b)
= –2sina sinb
\( = - 2\sin \frac{{u + v}}{2}\sin \frac{{u - v}}{2}\).
• sinu + sinv = sin(a + b) + sin(a – b)
= 2sina cosb
\( = 2\sin \frac{{u + v}}{2}\cos \frac{{u - v}}{2}\).
• sinu – sinv = sin(a + b) – sin(a – b)
= sin(b + a) + sin(b – a)
= 2sinb cosa = 2cosa sinb
\( = 2\cos \frac{{u + v}}{2}\sin \frac{{u - v}}{2}\).
Câu 17:
Tính: \[D = \frac{{\sin \frac{{7\pi }}{9} + \sin \frac{\pi }{9}}}{{{\rm{cos}}\frac{{7\pi }}{9} - \cos \frac{\pi }{9}}}\].
 Xem đáp án
Xem đáp án
Áp dụng công thức biến đổi tổng thành tích ta có:
\[\sin \frac{{7\pi }}{9} + \sin \frac{\pi }{9} = 2\sin \frac{{\frac{{7\pi }}{9} + \frac{\pi }{9}}}{2}\cos \frac{{\frac{{7\pi }}{9} - \frac{\pi }{9}}}{2} = 2\sin \frac{{4\pi }}{9}\cos \frac{\pi }{3}\];
\[{\rm{cos}}\frac{{7\pi }}{9} - \cos \frac{\pi }{9} = - 2\sin \frac{{\frac{{7\pi }}{9} + \frac{\pi }{9}}}{2}\sin \frac{{\frac{{7\pi }}{9} - \frac{\pi }{9}}}{2} = - 2\sin \frac{{4\pi }}{9}\sin \frac{\pi }{3}\].
Khi đó: \[D = \frac{{\sin \frac{{7\pi }}{9} + \sin \frac{\pi }{9}}}{{{\rm{cos}}\frac{{7\pi }}{9} - \cos \frac{\pi }{9}}}\]
\( = \frac{{2\sin \frac{{4\pi }}{9}\cos \frac{\pi }{3}}}{{ - 2\sin \frac{{4\pi }}{9}\sin \frac{\pi }{3}}} = - \frac{{\cos \frac{\pi }{3}}}{{\sin \frac{\pi }{3}}} = - \cot \frac{\pi }{3} = - \frac{{\sqrt 3 }}{3}\).
Câu 18:
Cho \(\cos a = \frac{3}{5}\) với \(0 < a < \frac{\pi }{2}\). Tính \(\sin \left( {a + \frac{\pi }{6}} \right),cos\left( {a - \frac{\pi }{3}} \right),\tan \left( {a + \frac{\pi }{4}} \right)\).
 Xem đáp án
Xem đáp án
Do \(0 < a < \frac{\pi }{2}\) nên \(\sin a > 0\).
Áp dụng công thức sin2a + cos2a = 1, ta có:
\[si{n^2}a + {\left( {\frac{3}{5}} \right)^2} = 1\]
\( \Rightarrow si{n^2}a = 1 - {\left( {\frac{3}{5}} \right)^2} = 1 - \frac{9}{{25}} = \frac{{16}}{{25}}\)
\[ \Rightarrow \sin a = \frac{4}{5}\] (do sina > 0).
Khi đó \(\tan a = \frac{{\sin a}}{{\cos a}} = \frac{{\frac{4}{5}}}{{\frac{3}{5}}} = \frac{4}{3}\).
Áp dụng công thức cộng, ta có:
• \(\sin \left( {a + \frac{\pi }{6}} \right) = \sin a\cos \frac{\pi }{6} + \cos a\sin \frac{\pi }{6} = \frac{4}{5}.\frac{{\sqrt 3 }}{2} + \frac{3}{5}.\frac{1}{2} = \frac{{4\sqrt 3 + 3}}{{10}}\);
• \(cos\left( {a - \frac{\pi }{3}} \right) = \cos a\,cos\frac{\pi }{3} + \sin a\sin \frac{\pi }{3} = \frac{3}{5}.\frac{1}{2} + \frac{4}{5}.\frac{{\sqrt 3 }}{2} = \frac{{3 + 4\sqrt 3 }}{{10}}\);
• \(\tan \left( {a + \frac{\pi }{4}} \right) = \frac{{\tan a + \tan \frac{\pi }{4}}}{{1 - \tan a\tan \frac{\pi }{4}}} = \frac{{\frac{4}{3} + 1}}{{1 - \frac{4}{3}.1}} = \frac{{\frac{7}{3}}}{{ - \frac{1}{3}}} = - 7\).
Câu 19:
Tính:
A = sin(a – 17°)cos(a + 13°) – sin(a + 13°)cos(a – 17°);
\(B = cos\left( {b + \frac{\pi }{3}} \right)\cos \left( {\frac{\pi }{6} - b} \right) - \sin \left( {b + \frac{\pi }{3}} \right)\sin \left( {\frac{\pi }{6} - b} \right)\).
 Xem đáp án
Xem đáp án
Ta có:
A = sin(a – 17°)cos(a + 13°) – sin(a + 13°)cos(a – 17°)
= sin(a – 17°)cos(a + 13°) – cos(a – 17°)sin(a + 13°)
= sin[(a – 17°) – (a + 13°)]
= sin(a – 17° – a – 13°)
= sin(‒30°)
= ‒ sin30°
\( = - \frac{1}{2}\).
\(B = cos\left( {b + \frac{\pi }{3}} \right)\cos \left( {\frac{\pi }{6} - b} \right) - \sin \left( {b + \frac{\pi }{3}} \right)\sin \left( {\frac{\pi }{6} - b} \right)\)
\[ = cos\left[ {\left( {b + \frac{\pi }{3}} \right) + \left( {\frac{\pi }{6} - b} \right)} \right]\]
\[ = cos\left[ {b + \frac{\pi }{3} + \frac{\pi }{6} - b} \right]\]
\[ = cos\frac{\pi }{2} = 0\].
Câu 20:
Cho tan(a + b) = 3, tan(a – b) = 2. Tính: tan2a, tan2b.
 Xem đáp án
Xem đáp án
Ta có:
tan2a = tan[(a + b) + (a – b)]
\( = \frac{{\tan \left( {a + b} \right) + \tan \left( {a - b} \right)}}{{1 - \tan \left( {a + b} \right)\tan \left( {a - b} \right)}} = \frac{{3 + 2}}{{1 - 3.2}} = \frac{5}{{ - 5}} = - 1\);
tan2b = tan[(a + b) ‒ (a – b)]
\( = \frac{{\tan \left( {a + b} \right) - \tan \left( {a - b} \right)}}{{1 + \tan \left( {a + b} \right)\tan \left( {a - b} \right)}} = \frac{{3 - 2}}{{1 + 3.2}} = \frac{1}{7}\).
Câu 21:
Cho \(\sin a = \frac{2}{{\sqrt 5 }}\). Tính cos2a, cos4a.
 Xem đáp án
Xem đáp án
Áp dụng công thức nhân đôi, ta có:
cos2a = 1 – 2sin2a = \(1 - 2.{\left( {\frac{2}{{\sqrt 5 }}} \right)^2} = 1 - 2.\frac{4}{5} = - \frac{3}{5}\).
cos4a = 2cos22a – 1 = \(2.{\left( { - \frac{3}{5}} \right)^2} - 1 = 2.\frac{9}{{25}} - 1 = - \frac{7}{{25}}\).
Câu 22:
Cho sina + cosa = 1. Tính: sin2a.
 Xem đáp án
Xem đáp án
Ta có: sina + cosa = 1
Þ (sina + cosa)2 = 12
Þ sin2a + 2sina cosa + cos2a = 1
Þ 2sina cosa + (sin2a + cos2a) = 1
Þ sin2a + 1 = 1
Þ sin2a = 0.
Vậy với sina + cosa = 1 thì sin2a = 0.
Câu 23:
Cho \(cos2a = \frac{1}{3}\) với \(\frac{\pi }{2} < a < \pi \). Tính: sina, cosa, tana.
 Xem đáp án
Xem đáp án
Do \(\frac{\pi }{2} < a < \pi \) nên cosa < 0 và sina > 0.
Áp dụng công thức hạ bậc ta có:
• \({\sin ^2}a = \frac{{1 - \cos 2a}}{2} = \frac{{1 - \frac{1}{3}}}{2} = \frac{1}{3}\) \( \Rightarrow \sin a = \frac{{\sqrt 3 }}{3}\) (do sina > 0).
• \({\cos ^2}a = \frac{{1 + \cos 2a}}{2} = \frac{{1 + \frac{1}{3}}}{2} = \frac{2}{3}\) \( \Rightarrow \cos a = - \frac{{\sqrt 6 }}{3}\) (do cosa < 0).
Khi đó: \(\tan a = \frac{{\sin a}}{{\cos a}} = \frac{{\frac{{\sqrt 3 }}{3}}}{{ - \frac{{\sqrt 6 }}{3}}}\)\( = - \frac{{\sqrt 2 }}{2}\).
Vậy \(\sin a = \frac{{\sqrt 3 }}{3},\cos a = - \frac{{\sqrt 6 }}{3}\) và \(\tan a = - \frac{{\sqrt 2 }}{2}\).
Câu 24:
Cho \(cos2x = \frac{1}{4}\). Tính: \(A = \cos \left( {x + \frac{\pi }{6}} \right)\cos \left( {x - \frac{\pi }{6}} \right)\); \(B = \sin \left( {x + \frac{\pi }{3}} \right)\sin \left( {x - \frac{\pi }{3}} \right)\).
 Xem đáp án
Xem đáp án
Ta có:
\[A = \cos \left( {x + \frac{\pi }{6}} \right)\cos \left( {x - \frac{\pi }{6}} \right)\]
\[ = \frac{1}{2}\left[ {\cos \left( {x + \frac{\pi }{6} + x - \frac{\pi }{6}} \right) + \cos \left( {x + \frac{\pi }{6} - x + \frac{\pi }{6}} \right)} \right]\]
\[ = \frac{1}{2}\left[ {\cos 2x + \cos \frac{\pi }{3}} \right]\]
\[ = \frac{1}{2}\left[ {\frac{1}{4} + \frac{1}{2}} \right] = \frac{3}{8}\].
\(B = \sin \left( {x + \frac{\pi }{3}} \right)\sin \left( {x - \frac{\pi }{3}} \right)\)
\[ = - \frac{1}{2}\left[ {\cos \left( {x + \frac{\pi }{3} + x - \frac{\pi }{3}} \right) - \cos \left( {x + \frac{\pi }{3} - x + \frac{\pi }{3}} \right)} \right]\]
\[ = - \frac{1}{2}\left[ {\cos 2x - \cos \frac{{2\pi }}{3}} \right]\]
\[ = - \frac{1}{2}\left[ {\frac{1}{4} - \left( { - \frac{1}{2}} \right)} \right] = - \frac{3}{8}\].
Vậy \(A = \frac{3}{8},B = - \frac{3}{8}\).
Câu 25:
Rút gọn biểu thức: \(A = \frac{{\sin 2x}}{{1 + \cos 2x}}\).
 Xem đáp án
Xem đáp án
Khi các biểu thức đều có nghĩa, ta có:
\(A = \frac{{\sin 2x}}{{1 + \cos 2x}}\)
\( = \frac{{2\sin x\cos x}}{{1 + \left( {2{{\cos }^2}x - 1} \right)}}\) (sử dụng công thức nhân đôi)
\( = \frac{{2\sin x\cos x}}{{2{{\cos }^2}x}}\)
\( = \frac{{\sin x}}{{\cos x}} = \tan x\).
Vậy A = tan x.
Câu 26:
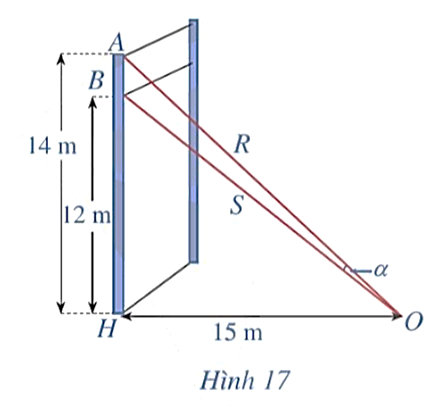
Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14 m. Một sợi cáp S khác cũng được gắn vào cột đó ở vị trí cách mặt đất 12 m. Biết rằng hai sợi cáp trên cùng được gắn với mặt đất tại một vị trí cách chân cột 15 m (Hình 17).
 Xem đáp án
Xem đáp án
Đặt \(\widehat {AOH} = \beta \).
Xét DAOH vuông tại H, ta có: \(\tan \beta = \frac{{AH}}{{HO}} = \frac{{14}}{{15}}\).
Đặt \(\widehat {BOH} = \gamma \)
Xét DBOH vuông tại H, ta có: \(\tan \gamma = \frac{{BH}}{{HO}} = \frac{{12}}{{15}} = \frac{4}{5}\).
\(\tan \alpha = \tan \left( {\beta - \widehat {BOH}} \right) = \tan \left( {\beta - \gamma } \right) = \frac{{\tan \beta - \tan \gamma }}{{1 + \tan \beta \tan \gamma }}\)
\( = \frac{{\frac{{14}}{{15}} - \frac{4}{5}}}{{1 + \frac{{14}}{{15}}.\frac{4}{5}}} = \frac{{\frac{2}{{15}}}}{{\frac{{131}}{{75}}}} = \frac{{10}}{{131}}\).
Vậy \(\tan \alpha = \frac{{10}}{{131}}\).
Câu 27:
Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14 m. Một sợi cáp S khác cũng được gắn vào cột đó ở vị trí cách mặt đất 12 m. Biết rằng hai sợi cáp trên cùng được gắn với mặt đất tại một vị trí cách chân cột 15 m (Hình 17).
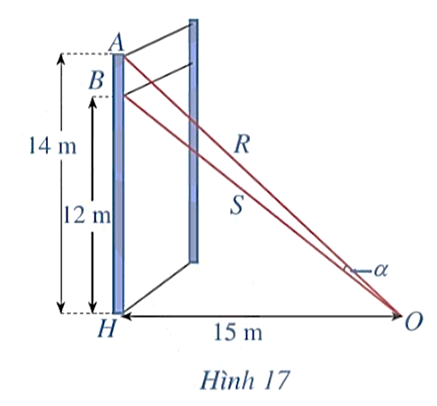
Tìm góc α (làm tròn kết quả đến hàng đơn vị theo đơn vị độ).
 Xem đáp án
Xem đáp án
Từ \(\tan \alpha = \frac{{10}}{{131}}\), để tìm số đo góc α, ta sử dụng máy tính cầm tay, trước tiên chuyển máy về chế độ “độ”, sau đó ấn lần lượt các nút:
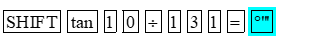
Ta được kết quả làm tròn kết quả đến hàng đơn vị theo đơn vị độ là 4°.
Vậy α ≈ 4°.
