Sử dụng công thức cộng đối với sin và côsin, hãy tính tan(a + b) theo tana và tanb khi các biểu thức đều có nghĩa.
Giải bởi Vietjack
Khi các biểu thức đều có nghĩa, ta có:
tan(a + b) \( = \frac{{\sin \left( {a + b} \right)}}{{cos\left( {a + b} \right)}} = \frac{{\sin a\cos b + \cos a\sin b}}{{\cos a\cos b - \sin a\sin b}}\)
\[ = \frac{{\frac{{\sin a\cos b + \cos a\sin b}}{{\cos a\cos b}}}}{{\frac{{\cos a\cos b - \sin a\sin b}}{{\cos a\cos b}}}}\] (chia cả tử và mẫu cho cosacosb)
\[ = \frac{{\frac{{\sin a\cos b}}{{\cos a\cos b}} + \frac{{\cos a\sin b}}{{\cos a\cos b}}}}{{\frac{{\cos a\cos b}}{{\cos a\cos b}} - \frac{{\sin a\sin b}}{{\cos a\cos b}}}}\]
\[ = \frac{{\frac{{\sin a}}{{\cos a}} + \frac{{\sin b}}{{\cos b}}}}{{1 - \frac{{\sin a}}{{\cos a}}.\frac{{\sin b}}{{\cos b}}}}\]
\[ = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\]
Vậy \[\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\].
Cho \(cos2x = \frac{1}{4}\). Tính: \(A = \cos \left( {x + \frac{\pi }{6}} \right)\cos \left( {x - \frac{\pi }{6}} \right)\); \(B = \sin \left( {x + \frac{\pi }{3}} \right)\sin \left( {x - \frac{\pi }{3}} \right)\).
Cho \(\cos a = \frac{3}{5}\) với \(0 < a < \frac{\pi }{2}\). Tính \(\sin \left( {a + \frac{\pi }{6}} \right),cos\left( {a - \frac{\pi }{3}} \right),\tan \left( {a + \frac{\pi }{4}} \right)\).
Cho \(cos2a = \frac{1}{3}\) với \(\frac{\pi }{2} < a < \pi \). Tính: sina, cosa, tana.
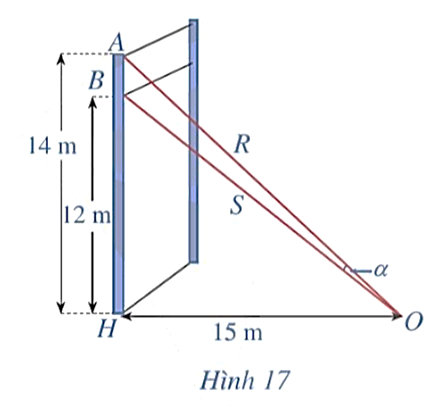
Tính: \[D = \frac{{\sin \frac{{7\pi }}{9} + \sin \frac{\pi }{9}}}{{{\rm{cos}}\frac{{7\pi }}{9} - \cos \frac{\pi }{9}}}\].
Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14 m. Một sợi cáp S khác cũng được gắn vào cột đó ở vị trí cách mặt đất 12 m. Biết rằng hai sợi cáp trên cùng được gắn với mặt đất tại một vị trí cách chân cột 15 m (Hình 17).
Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14 m. Một sợi cáp S khác cũng được gắn vào cột đó ở vị trí cách mặt đất 12 m. Biết rằng hai sợi cáp trên cùng được gắn với mặt đất tại một vị trí cách chân cột 15 m (Hình 17).
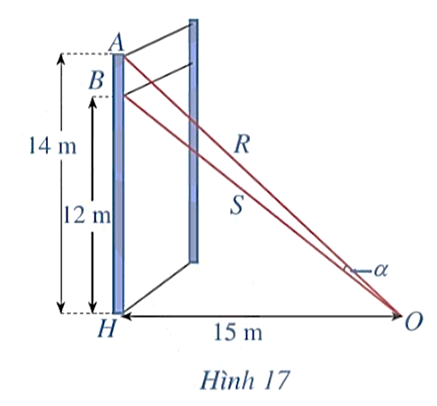
Tìm góc α (làm tròn kết quả đến hàng đơn vị theo đơn vị độ).
Khi các biểu thức đều có nghĩa, hãy tính tan (a – b) bằng cách biến đổi \[tan\left( {a - b} \right) = tan\left[ {a + \left( { - b} \right)} \right]\] và sử dụng công thức tan(a + b) có được ở bài trước
Tính cos(a + b) bằng cách biến đổi cos(a + b) = \(\sin \left[ {\frac{\pi }{2} - \left( {a + b} \right)} \right] = \sin \left[ {\left( {\frac{\pi }{2} - a} \right) - b} \right]\) và sử dụng công thức cộng đối với sin.
Cho \(a = \frac{\pi }{6},b = \frac{\pi }{3}\). Hãy tính sina, cosa, sinb, cosb và sin(a + b). Từ đó rút ra đẳng thức sin(a + b) = sina cosb + cosa sinb (*).
