38 câu hỏi trắc nghiệm thuộc Đề kiểm tra Cuối kì 1 Toán 11 KNTT có đáp án - Đề 01

Câu 1:

Trên đường tròn lượng giác, gọi $M\left( {{x_0};{y_0}} \right)$ là điểm biểu diễn cho góc lượng giác có số đo $\alpha $. Mệnh đề nào đúng trong các mệnh đề sau?

A. $\sin \alpha = {y_0}$.

B. $\sin \alpha = {x_0}$.

C. $\sin \alpha = - {x_0}$.

D. $\sin \alpha = - {y_0}$.

Xem đáp án

Chọn A

Câu 2:

Hàm số nào sau đây là hàm số tuần hoàn với chu kì $\pi $.

A. $y = \sin x$.

B. $y = \cos x$.

C. $y = \tan 2x$.

D. $y = \cot x$.

Xem đáp án

Chọn D

Câu 3:

Cho hàm số $y = f\left( x \right)$ có đồ thị là hình vẽ dưới đây

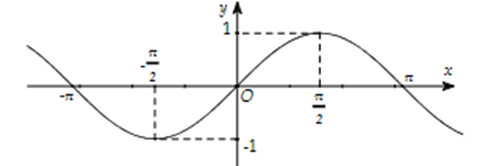
Cho hàm số y = f(x) có đồ thị là hình vẽ dưới đây (ảnh 1)

Khẳng định nào sau đây đúng?

A. Hàm số đồng biến trên $\left( { - \pi ;0} \right)$.

B. Hàm số nghịch biến trên $\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)$.

C. Hàm số đồng biến trên $\left( {0;\pi } \right)$.

D. Hàm số đồng biến trên $\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)$.

Xem đáp án

Chọn D

Câu 4:

Tìm nghiệm của phương trình $2\sin x - 3 = 0$.

A. $x \in \emptyset $.

B. $\left[ \begin{gathered}

x = \arcsin \frac{3}{2} + k2\pi \hfill \\

x = \pi - \arcsin \frac{3}{2} + k2\pi \hfill \\

\end{gathered} \right.\left( {k \in \mathbb{Z}} \right)$.

C. $\left[ \begin{gathered}

x = \arcsin \frac{3}{2} + k2\pi \hfill \\

x = - \arcsin \frac{3}{2} + k2\pi \hfill \\

\end{gathered} \right.\left( {k \in \mathbb{Z}} \right)$.

D. $x \in \mathbb{R}$.

Xem đáp án

Chọn A

Câu 5:

Phương trình \[\tan x = - 1\] có nghiệm là

A. $x = \frac{\pi }{4} + k\pi ,k \in \mathbb{Z}$.

B. $x = - \frac{\pi }{4} + k2\pi ,k \in \mathbb{Z}$.

C. $x = \frac{\pi }{4} + k2\pi ,k \in \mathbb{Z}$.

D. $x = - \frac{\pi }{4} + k\pi ,k \in \mathbb{Z}$.

Xem đáp án

Chọn D

Câu 6:

Trong các dãy số $\left( {{u_n}} \right)$ cho bởi số hạng tổng quát ${u_n}$ sau, dãy số nào giảm?

A. ${u_n} = {\left( {\frac{4}{3}} \right)^n}$.

B. ${u_n} = {\left( { - 1} \right)^n}\left( {{5^n} - 1} \right)$.

C. ${u_n} = - {3^n}$.

D. ${u_n} = \sqrt {n + 4} $.

Xem đáp án

Chọn C

Câu 7:

Xét tính bị chặn của dãy số sau: ${u_n} = 3n - 1$.

A. Bị chặn.

B. Bị chặn trên.

C. Bị chặn dưới.

D. Không bị chặn dưới.

Xem đáp án

Chọn C

Câu 8:

Cho dãy số $\left( {{u_n}} \right)$, biết \[{u_n} = \frac{{2n + 1}}{{n + 2}}\]. Viết năm số hạng đầu của dãy số.

A. ${u_1} = 1;{u_2} = \frac{3}{4};{u_3} = \frac{7}{5};{u_4} = \frac{3}{2};{u_5} = \frac{{11}}{7}$.

B. ${u_1} = 1;{u_2} = \frac{5}{4};{u_3} = \frac{7}{5};{u_4} = \frac{3}{2};{u_5} = \frac{{11}}{7}$.

C. ${u_1} = 1;{u_2} = \frac{5}{4};{u_3} = \frac{8}{5};{u_4} = \frac{3}{2};{u_5} = \frac{{11}}{7}$.

D. ${u_1} = 1;{u_2} = \frac{5}{4};{u_3} = \frac{7}{5};{u_4} = \frac{7}{2};{u_5} = \frac{{11}}{3}$.

Xem đáp án

Chọn B

Câu 9:

Trong các dãy số sau đây, dãy số nào là cấp số cộng?

A. ${u_n} = 3{n^2} + 2017$.

B. ${u_n} = 3n + 2008$.

C. ${u_n} = {3^n}$.

D. ${u_n} = {\left( { - 3} \right)^{n + 1}}$.

Xem đáp án

Chọn B

Câu 10:

Cho một cấp số cộng $\left( {{u_n}} \right)$ có ${u_1} = \frac{1}{3};{u_8} = 26$. Tìm công sai $d$.

A. $d = \frac{{11}}{3}$.

B. $d = \frac{{10}}{3}$.

C. $d = \frac{3}{{10}}$.

D. $d = \frac{3}{{11}}$.

Xem đáp án

Chọn A

Câu 11:

Cho một cấp số cộng $\left( {{u_n}} \right)$ có ${u_1} = 5$ và tổng của 50 số hạng đầu bằng 5 150. Tìm công thức của số hạng tổng quát ${u_n}$.

A. ${u_n} = 1 + 4n$.

B. ${u_n} = 5n$.

C. ${u_n} = 3 + 2n$.

D. ${u_n} = 2 + 3n$.

Xem đáp án

Chọn A

Câu 12:

Cho dãy số $ - 1;1; - 1;1; - 1;...$ Khẳng định nào sau đây là đúng?

A. Dãy số này không phải là cấp số nhân.

B. Số hạng tổng quát ${u_n} = {1^n} = 1$.

C. Dãy số này là cấp số nhân có ${u_1} = - 1;q = - 1$.

D. Số hạng tổng quát ${u_n} = {\left( { - 1} \right)^{2n}}$.

Xem đáp án

Chọn C

Câu 13:

Cho cấp số nhân $\left( {{u_n}} \right)$ có ${u_n} = 81$ và ${u_{n + 1}} = 9$. Mệnh đề nào sau đây đúng?

A. $q = \frac{1}{9}$.

B. $q = 9$.

C. $q = - 9$.

D. $q = - \frac{1}{9}$.

Xem đáp án

Chọn A

Câu 14:

Cho cấp số nhân $\frac{1}{2};\frac{1}{4};\frac{1}{8};...;\frac{1}{{4096}}$. Hỏi số $\frac{1}{{4096}}$ là số hạng thứ mấy trong cấp số nhân đã cho?

A. $11$.

B. $12$.

C. $10$.

D. $13$.

Xem đáp án

Chọn B

Câu 15:

Cho dãy số $\left( {{u_n}} \right)$ thỏa mãn $\left| {{u_n} - 2} \right| < \frac{1}{{{n^3}}}$ với mọi $n \in {\mathbb{N}^*}$. Khi đó

A. $\mathop {\lim }\limits_{n \to + \infty } {u_n}$ không tồn tại.

B. $\mathop {\lim }\limits_{n \to + \infty } {u_n} = 1$.

C. $\mathop {\lim }\limits_{n \to + \infty } {u_n} = 0$.

D. $\mathop {\lim }\limits_{n \to + \infty } {u_n} = 2$.

Xem đáp án

Chọn D

Câu 16:

$\mathop {\lim }\limits_{n \to + \infty } \frac{1}{{5n + 3}}$ bằng

A. 0.

B. $\frac{1}{3}$.

C. $ + \infty $.

D. $\frac{1}{5}$.

Xem đáp án

Chọn A

Câu 17:

$\mathop {\lim }\limits_{n \to + \infty } \frac{{\sqrt {4{n^2} + 1} - \sqrt {n + 2} }}{{2n - 3}}$ bằng

A. $\frac{3}{2}$.

B. $2$.

C. $1$.

D. $ + \infty $.

Xem đáp án

Chọn C

Câu 18:

Giá trị của $\mathop {\lim }\limits_{x \to 1} \left( {2{x^2} - 3x + 1} \right)$ bằng

A. $2$.

B. $1$.

C. $ + \infty $.

D. $0$.

Xem đáp án

Chọn D

Câu 19:

Tìm giới hạn \[\mathop {\lim }\limits_{x \to {1^ + }} \frac{{4x - 3}}{{x - 1}}\].

A. $ + \infty $.

B. $2$.

C. $ - \infty $.

D. $ - 2$.

Xem đáp án

Chọn A

Câu 20:

Trong các mệnh đề sau, mệnh đề nào sai?

A. $\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} - x + 1} + x - 2} \right) = - \frac{3}{2}$.

B. $\mathop {\lim }\limits_{x \to - {1^ - }} \frac{{3x + 2}}{{x + 1}} = - \infty $.

C. $\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} - x + 1} + x - 2} \right) = + \infty $.

D. $\mathop {\lim }\limits_{x \to - {1^ + }} \frac{{3x + 2}}{{x + 1}} = - \infty $.

Xem đáp án

Chọn B

Câu 21:

Hàm số nào sau đây liên tục tại $x = 1$.

A. $\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} - x + 1} + x - 2} \right) = - \frac{3}{2}$.

B. $f\left( x \right) = \frac{{{x^2} - x - 2}}{{{x^2} - 1}}$.

C. $f\left( x \right) = \frac{{{x^2} + x + 1}}{x}$.

D. $f\left( x \right) = \frac{{x + 1}}{{x - 1}}$.

Xem đáp án

Chọn C

Câu 22:

Trong các hàm số sau, hàm số nào liên tục trên $\mathbb{R}$.

A. $f\left( x \right) = \tan x + 5$.

B. $f\left( x \right) = \frac{{{x^2} + 3}}{{5 - x}}$.

C. $f\left( x \right) = \sqrt {x - 6} $.

D. $f\left( x \right) = \frac{{x + 5}}{{{x^2} + 4}}$.

Xem đáp án

Chọn D

Câu 23:

Cho hai đường thẳng $a,b$ cắt nhau và không đi qua điểm $A$. Xác định nhiều nhất bao nhiêu mặt phẳng bởi $a,b$ và $A$?

A. $1$.

B. $2$.

C. $3$.

D. $4$.

Xem đáp án

Chọn C

Câu 24:

Chọn khẳng định sai?

A. Hai mặt phẳng có một điểm chung thì chúng còn có vô số điểm chung khác nữa.

B. Hai mặt phẳng có một điểm chung thì chúng có một đường thẳng chung duy nhất.

C. Hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất.

D. Nếu ba điểm phân biệt $M,N,P$ cùng thuộc hai mặt phẳng phân biệt thì chúng thẳng hàng.

Xem đáp án

Chọn B

Câu 25:

Cho 5 điểm $A,B,C,D,E$ trong đó không có 4 điểm ở trên một mặt phẳng. Hỏi có bao nhiêu mặt phẳng tạo bởi 3 trong 5 điểm đã cho?

A. 10.

B. 12.

C. 8.

D. 14.

Xem đáp án

Chọn A

Câu 26:

Cho hình chóp $S.ABCD$. Gọi $I$ là trung điểm của $SD$, $J$ là điểm trên $SC$ và không trùng trung điểm $SC$. Giao tuyến của hai mặt phẳng $\left( {ABCD} \right)$ và $\left( {AIJ} \right)$ là

A. $AK$, $K$ là giao điểm của $IJ$ và $BC$.

B. $AH$, $H$ là giao điểm của $IJ$ và $AB$.

C. $AG$, $G$ là giao điểm của $IJ$ và $AD$.

D. $AF$, $F$ là giao điểm của $IJ$ và $CD$.

Xem đáp án

Chọn D

Câu 27:

Cho các mệnh đề sau:

1) Hai đường thẳng song song thì đồng phẳng.

2) Hai đường thẳng không có điểm chung thì chéo nhau.

3) Hai đường thẳng chéo nhau thì không có điểm chung.

4) Hai đường thẳng chéo nhau thì không đồng phẳng.

Có bao nhiêu mệnh đề đúng?

A. 1.

B. 2.

C. 3.

D. 4.

Xem đáp án

Chọn C

Câu 28:

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $\Delta $ là giao tuyến chung của hai mặt phẳng $\left( {SAD} \right)$ và $\left( {SBC} \right)$. Đường thẳng $\Delta $ song song với đường thẳng nào dưới đây?

A. Đường thẳng $AB$.

B. Đường thẳng $AD$.

C. Đường thẳng $AC$.

D. Đường thẳng $SA$.

Xem đáp án

Chọn B

Câu 29:

Cho đường thẳng $d$ song song với mặt phẳng $\left( P \right)$. Mệnh đề nào sau đây đúng?

C. Đường thẳng $d$ có đúng hai điểm chung với mặt phẳng $\left( P \right)$.

D. Đường thẳng $d$ có vô số điểm chung với mặt phẳng $\left( P \right)$.

Xem đáp án

Chọn A

Câu 30:

Cho tứ diện $ABCD$. Gọi hai điểm $M,\,N$ lần lượt là trung điểm của các cạnh $AB,\,AC$. Đường thẳng $MN$ song song với mặt phẳng nào sau đây?

A. Mặt phẳng $\left( {ABD} \right)$.

B. Mặt phẳng $\left( {ACD} \right)$.

C. Mặt phẳng $\left( {ABC} \right)$.

D. Mặt phẳng $\left( {BCD} \right)$.

Xem đáp án

Chọn D

Câu 31:

Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Gọi $M,N$ lần lượt là trung điểm của $SA$ và $AB$. Khẳng định nào sau đây đúng?

A. $MN{\text{//}}\left( {SBC} \right)$.

B. $MN{\text{//}}BD$.

C. $MN{\text{//}}\left( {SAB} \right)$.

D. $MN$ cắt $BC$.

Xem đáp án

Chọn A

Câu 32:

Trong các mệnh đề sau, mệnh đề nào đúng?

A. Nếu hai mặt phẳng $\left( \alpha \right)$ và $\left( \beta \right)$ song song với nhau thì mọi đường thẳng nằm trong $\left( \alpha \right)$ đều song song với $\left( \beta \right)$.

B. Nếu hai mặt phẳng $\left( \alpha \right)$ và $\left( \beta \right)$ song song với nhau thì bất kì đường thẳng nào nằm trong $\left( \alpha \right)$ cũng song song với bất kì đường thẳng nào nằm trong $\left( \beta \right)$.

C. Nếu hai đường thẳng phân biệt $a$ và $b$ song song lần lượt nằm trong hai mặt phẳng $\left( \alpha \right)$ và $\left( \beta \right)$ phân biệt thì $\left( \alpha \right){\text{//}}\left( \beta \right)$.

D. Nếu đường thẳng $d$ song song với $\left( \alpha \right)$ thì nó song song với mọi đường thẳng nằm trong $\left( \alpha \right)$.

Xem đáp án

Chọn A

Câu 33:

Cho hình hộp $ABCD.A'B'C'D'$(tham khảo hình vẽ bên dưới)

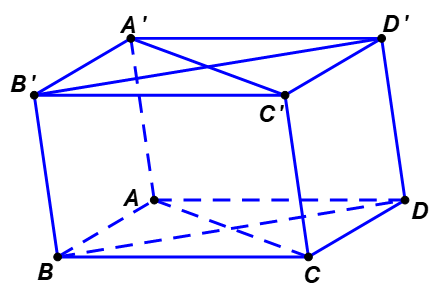
Cho hình hộp ABCD.A'B'C'D' (tham khảo hình vẽ (ảnh 1)

Mệnh đề nào sau đây sai?

A. $\left( {BDD'B'} \right)\;{\text{//}}\;\left( {ACC'A'} \right)$.

B. $\left( {AA'D'D} \right)\;{\text{//}}\;\left( {BCC'B'} \right)$.

C. $\left( {ABCD} \right)\;{\text{//}}\;\left( {A'B'C'D'} \right)$.

D. $\left( {ABB'A'} \right)\;{\text{//}}\;\left( {CDD'C'} \right)$.

Xem đáp án

Chọn A

Câu 34:

Qua phép chiếu song song biến ba đường thẳng song song thành

A. Ba đường thẳng đôi một song song với nhau.

B. Một đường thẳng.

C. Hai đường thẳng song song.

D. Cả ba trường hợp trên.

Xem đáp án

Chọn D

Câu 35:

Cho tam giác $ABC$ ở trong mặt phẳng $\left( \alpha \right)$ và phương $l$. Biết hình chiếu (theo phương $l$) của tam giác $ABC$ lên mặt phẳng $\left( P \right)$ là một đoạn thẳng. Khẳng định nào sau đây đúng?

A. $\left( \alpha \right){\text{//}}\left( P \right)$.

B. $\left( \alpha \right) \equiv \left( P \right)$.

C. $\left( \alpha \right){\text{//}}\,l$ hoặc $l \subset \left( \alpha \right)$.

D. Cả A, B, C đều sai.

Xem đáp án

Chọn C

Câu 36:

Cho cấp số nhân $\left( {{u_n}} \right)$ biết ${u_1} = 12;\frac{{{u_3}}}{{{u_8}}} = 243$. Tìm ${u_9}$.

Xem đáp án

Gọi $q$ là công bội của cấp số nhân.

Ta có $\frac{{{u_3}}}{{{u_8}}} = \frac{{{u_1}{q^2}}}{{{u_1}{q^7}}} = 243 $\Leftrightarrow \frac{1}{{{q^5}}} = 243$ \Leftrightarrow q = \frac{1}{3}$.

Có ${u_9} = {u_1}{q^8}$$ = 12 \cdot {\left( {\frac{1}{3}} \right)^8} = \frac{4}{{2187}}$.

Câu 37:

Tính giới hạn $\mathop {\lim }\limits_{x \to 1} \frac{{2\sqrt {x + 3} + x - 5}}{{x - {x^2}}}$.

Xem đáp án

$\mathop {\lim }\limits_{x \to 1} \frac{{2\sqrt {x + 3} + x - 5}}{{x - {x^2}}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left[ {2\sqrt {x + 3} + \left( {x - 5} \right)} \right]\left[ {2\sqrt {x + 3} - \left( {x - 5} \right)} \right]}}{{\left( {x - {x^2}} \right)\left( {2\sqrt {x + 3} - \left( {x - 5} \right)} \right)}}$

$ = \mathop {\lim }\limits_{x \to 1} \frac{{ - {x^2} + 14x - 13}}{{ - x\left( {x - 1} \right)\left( {2\sqrt {x + 3} - \left( {x - 5} \right)} \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{ - \left( {x - 1} \right)\left( {x - 13} \right)}}{{ - x\left( {x - 1} \right)\left( {2\sqrt {x + 3} - \left( {x - 5} \right)} \right)}}$

$ = \mathop {\lim }\limits_{x \to 1} \frac{{ - \left( {x - 13} \right)}}{{ - x\left( {2\sqrt {x + 3} - \left( {x - 5} \right)} \right)}} = - \frac{3}{2}$.

Câu 38:

Tam giác mà ba đỉnh của nó là ba trung điểm ba cạnh của tam giác $ABC$ được gọi là tam giác trung bình của tam giác $ABC$. Ta xây dựng dãy các tam giác ${A_1}{B_1}{C_1};{A_2}{B_2}{C_2};{A_3}{B_3}{C_3};...$ sao cho ${A_1}{B_1}{C_1}$ là một tam giác đều cạnh bằng 3 và với mỗi số nguyên dương $n \geqslant 2$, tam giác ${A_n}{B_n}{C_n}$ là tam giác trung bình của tam giác ${A_{n - 1}}{B_{n - 1}}{C_{n - 1}}$. Với mỗi số nguyên dương $n$, kí hiệu ${S_n}$ tương ứng là diện tích hình tròn ngoại tiếp tam giác ${A_n}{B_n}{C_n}$. Tính tổng $S = {S_1} + {S_2} + ... + {S_n} + ...$.

Xem đáp án

Vì dãy các tam giác ${A_1}{B_1}{C_1};{A_2}{B_2}{C_2};{A_3}{B_3}{C_3};...$ là các tam giác đều nên bán kính đường tròn ngoại tiếp các tam giác bằng cạnh $ \times \frac{{\sqrt 3 }}{3}$.

Với $n = 1$ thì tam giác đều ${A_1}{B_1}{C_1}$ có cạnh bằng 3 nên bán kính đường tròn ngoại tiếp tam giác đều ${A_1}{B_1}{C_1}$ là ${R_1} = 3 \cdot \frac{{\sqrt 3 }}{3} = \sqrt 3 $. Do đó ${S_1} = \pi {\left( {\sqrt 3 } \right)^2} = 3\pi $.

Với $n = 2$ thì tam giác đều ${A_2}{B_2}{C_2}$ có cạnh bằng $\frac{3}{2}$ nên bán kính đường tròn ngoại tiếp tam giác đều ${A_2}{B_2}{C_2}$ là ${R_2} = \frac{3}{2} \cdot \frac{{\sqrt 3 }}{3} = \frac{{\sqrt 3 }}{2}$. Do đó ${S_2} = \pi {\left( {\frac{{\sqrt 3 }}{2}} \right)^2} = 3\pi \cdot \frac{1}{4}$.

Với $n = 3$ thì tam giác đều ${A_3}{B_3}{C_3}$ có cạnh bằng $\frac{3}{4}$ nên bán kính đường tròn ngoại tiếp tam giác đều ${A_3}{B_3}{C_3}$ là ${R_3} = \frac{3}{4} \cdot \frac{{\sqrt 3 }}{3} = \frac{{\sqrt 3 }}{4}$. Do đó ${S_3} = \pi {\left( {\frac{{\sqrt 3 }}{4}} \right)^2} = 3\pi {\left( {\frac{1}{4}} \right)^2}$.

Như vậy tam giác ${A_n}{B_n}{C_n}$ có cạnh $3 \cdot {\left( {\frac{1}{2}} \right)^{n - 1}}$ và bán kính đường tròn ngoại tiếp tam giác đều ${A_n}{B_n}{C_n}$ là \[{R_n} = 3 \cdot {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot \frac{{\sqrt 3 }}{3} = \sqrt 3 .{\left( {\frac{1}{2}} \right)^{n - 1}}\]. Do đó ${S_n} = \pi {\left( {\sqrt 3 .{{\left( {\frac{1}{2}} \right)}^{n - 1}}} \right)^2} = 3\pi {\left( {\frac{1}{4}} \right)^{n - 1}}$.

Khi đó $S = {S_1} + {S_2} + ... + {S_n} + ...$\[ = 3\pi + 3\pi \cdot \frac{1}{4} + 3\pi \cdot {\left( {\frac{1}{4}} \right)^2} + ... + 3\pi \cdot {\left( {\frac{1}{4}} \right)^{n - 1}} + ...\] là tổng cấp số nhân lùi vô hạn với ${u_1} = 3\pi ;q = \frac{1}{4}$.

Vậy $S = \frac{{{u_1}}}{{1 - q}} = \frac{{3\pi }}{{1 - \frac{1}{4}}} = 4\pi $.